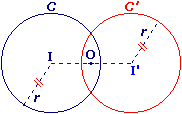
Pour construire le symétrique du cercle C par rapport à O :
- On place le symétrique I' du centre I.
- Puis on trace le cercle C' de centre I' et de rayon r.
 |
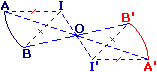
Pour construire le symétrique de l'arc de cercle 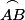 par rapport à O :
par rapport à O :
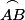 par rapport à O :
par rapport à O :- On place le symétrique I' du centre I de l'arc.
- On construit les images A' et B' de A et B.
- Pointe du compas sur I', crayon sur A', on trace l'arc
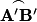 .
.
 |
Exercice n°1
Associe à chaque affirmation le commentaire qui convient.
Dans une symétrie de centre O :
Faites glisser les étiquettes dans les zones prévues à cet effet.
Pas forcément
Toujours
1. Si le cercle C' n'a pas le même rayon que le cercle C, alors C' n'est pas le symétrique de C.
→
→
imcAnswer2|imcAnswer3?
2. Si le cercle C' de centre J est le symétrique du cercle C de centre I, alors J est le symétrique de I.
→
→
imcAnswer2|imcAnswer3?
Dans une symétrie centrale :
1. Un cercle et son symétrique ont toujours le même rayon.
2. Deux cercles symétriques ont des centres symétriques l'un de l'autre.
Exercice n°2
Complète.
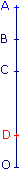 |
Écrivez les réponses dans les zones colorées.
1. On a DC = CA.
D est le symétrique de A par rapport au point .
D est le symétrique de A par rapport au point .
2. Un cercle de centre D et de rayon 7 cm est donc le symétrique, par rapport au point C, d'un cercle de centre et de rayon cm.
1. AC = CD.
A et D sont donc symétriques par rapport à C.
A et D sont donc symétriques par rapport à C.
2. Dans une symétrie centrale :
- un cercle et son symétrique ont le même rayon ;
- deux cercles symétriques ont des centres symétriques l'un de l'autre.
Exercice n°3
Coche la réponse exacte.
a. Dans une symétrie centrale, le symétrique d'un cercle est :
Cochez la bonne réponse.
| ||
| ||
|
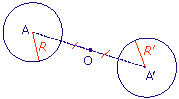
b. Si, dans une symétrie de centre O, le cercle C de centre A et de rayon R a pour symétrique le cercle C' de centre A' et de rayon R', alors laquelle des affirmations suivantes est fausse ?
Cochez la bonne réponse.
| ||
| ||
|
 |

