Propriété
Si un parallélogramme est à la fois un rectangle et un losange, c'est un carré.
Application
Si deux côtés consécutifs d'un parallélogramme sont à la fois perpendiculaires et de même longueur, ou si ses diagonales sont à la fois perpendiculaires et de même longueur, alors on peut dire que c'est un carré.
Exemple
[AB] et [CD] sont deux diamètres perpendiculaires d'un cercle de centre O.
Quelle est la nature du quadrilatère ACBD ?
Quelle est la nature du quadrilatère ACBD ?
 |
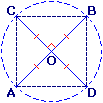- Les diagonales [AB] et [CD] ont le même milieu O donc ABCD est un parallélogramme.
- De plus, elles sont perpendiculaires et elles ont la même longueur donc ACBD est un carré.
Exercice n°1
ABCD est un parallélogramme.
Détermine quel type de quadrilatère correpond à chaque description.
Détermine quel type de quadrilatère correpond à chaque description.
Faites glisser les étiquettes dans les zones prévues à cet effet.
carré
rectangle
losange
1. Si (AD) 
(AB) et AD = AB, alors ABCD est un
(AB) et AD = AB, alors ABCD est un imcAnswer2|imcAnswer4?
. 2. Si (AD) 
(AB), alors ABCD est un
(AB), alors ABCD est un imcAnswer3?
. 3. Si (AC) 
(BD) et AC = BD, alors ABCD est un
(BD) et AC = BD, alors ABCD est un imcAnswer2|imcAnswer4?
. 1. Les côtés sont alors tous égaux et les angles, tous droits.
3. Les diagonales sont alors perpendiculaires et de même longueur.
Exercice n°2
 |
Lis les affirmations suivantes.
Laquelle de ces phrases est juste ?
Cochez la bonne réponse.
| ||
| ||
|
Un carré est un rectangle dont les quatre côtés sont de même longueur et dont les diagonales sont perpendiculaires.
Exercice n°3
Coche la réponse exacte.
a. Quelle phrase définit un carré ?
Cochez la bonne réponse.
| ||
| ||
|
b. Un carré possède ?
Cochez la bonne réponse.
| ||
| ||
|
 |
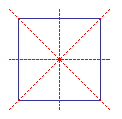Un carré a pour axes de symétrie ses médiatrices et ses diagonales. Son centre de symétrie est leur point d'intersection.
Exercice n°4
Trace un triangle EFG rectangle et isocèle en F puis construis les points H et L symétriques de E et G par rapport à F.
Complète ensuite la démonstration suivante.
Complète ensuite la démonstration suivante.
Écrivez les réponses dans les zones colorées.
F est le milieu de [E] et [] donc EGHL est un . Le triangle EFG étant rectangle et isocèle en F, les diagonales de EGHL sont p et é. Conclusion : EGHL est un .
• Un quadrilatère dont les diagonales ont le même milieu est un parallélogramme.
• Un parallélogramme dont les diagonales sont de même longueur et perpendiculaires est un carré.
