• Une suite d'additions et de soustractions de nombres relatifs peut être écrite uniquement à l'aide d'additions, c'est pourquoi on parle de somme algébrique.
Exemple : A = (–12) + 8 – 10 + (–4 ) – (–6).
Sachant que soustraire un nombre relatif revient à additionner son opposé, on peut réécrire A ainsi :
A = (–12) + 8 + (–10) + (–4) + 6.
• Rappel :
- a – (–b) = a + b
- a + (–b) = a – b
- (–a) + b = –a + b
On peut donc simplifier l'écriture d'une somme algébrique en l'écrivant sans parenthèses.
Exemple : A = (–12) + 8 – 10 + (–4) – (–6)
peut aussi s'écrire A = –12 + 8 – 10 – 4 + 6.
On effectue alors les calculs de la gauche vers la droite :
A = –4 – 10 – 4 + 6
A = –18 + 6 = –12
Exercice n°1
Complète par les nombres entre parenthèses, puis supprime les parenthèses avant de terminer le calcul.
Écrivez les réponses dans les zones colorées.
a. 24 − (− 9) + (− 51) = 24 + () + ()
24 − (− 9) + (− 51) = 24 + 9 51
24 − (− 9) + (− 51) =
24 − (− 9) + (− 51) = 24 + 9 51
24 − (− 9) + (− 51) =
b. − 13 + (− 27) − 7 = − 13 + () + ()
− 13 + (− 27) − 7 = − 13 27 7
− 13 + (− 27) − 7 =
− 13 + (− 27) − 7 = − 13 27 7
− 13 + (− 27) − 7 =
La soustraction d'un nombre relatif est transformée en l'addition de son opposé.
Ainsi − (− 9) devient + 9.
Ainsi − (− 9) devient + 9.
Exercice n°2
Effectue les calculs sur une feuille de brouillon. Écris ensuite le résultat.
Écrivez les réponses dans les zones colorées.
a. (− 1) + 7 + 8 + (− 4) + 6 + (− 4) =
b. 8 + (− 3,4) + (− 27,1) + 14 + 3,4 + (− 8) + 27,1 =
c. 24 + (− 28) + 12 + (− 16) + 10 + (− 14) =
d. 6 − 7,1 + 8 + 7,1 − 12,4 =
a.
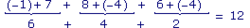 |
b. 8 + (− 3,4) + (− 27,1) + 14 + 3,4 + (− 8) + 27,1
= (− 27,1) + 27,1 + 8 + (− 8) + (− 3,4) + 3,4 + 14
= 0 + 0 + 0 + 14 = 14
= (− 27,1) + 27,1 + 8 + (− 8) + (− 3,4) + 3,4 + 14
= 0 + 0 + 0 + 14 = 14
c.
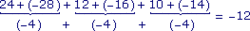 |
d. 6 − 7,1 + 8 + 7,1 − 12,4
= 6 + (− 7,1) + 8 + 7,1 + (− 12,4)
= 6 + 8 + (− 7,1) + 7,1 + (− 12,4)
= 14 + 0 + (− 12,4) = 1,6
= 6 + (− 7,1) + 8 + 7,1 + (− 12,4)
= 6 + 8 + (− 7,1) + 7,1 + (− 12,4)
= 14 + 0 + (− 12,4) = 1,6
Exercice n°3
Effectue les calculs après avoir remplacé chaque lettre par sa valeur.
a = 1 ; b = − 2 ; c = 7 ; d = − 9 ; e = − 3.
a = 1 ; b = − 2 ; c = 7 ; d = − 9 ; e = − 3.
Écrivez les réponses dans les zones colorées.
A = b + a − c − d =
B = c − e − d =
C = a − b + c − e =
D = b − a − d + e =
Si on remplace les lettres par les valeurs données, on obtient :
A = − 2 + 1 − 7 + 9
B = 7 + 3 + 9
C = 1 + 2 + 7 + 3
D = − 2 − 1 + 9 − 3
A = − 2 + 1 − 7 + 9
B = 7 + 3 + 9
C = 1 + 2 + 7 + 3
D = − 2 − 1 + 9 − 3
Exercice n°4
Un ascenseur part du 3e étage, il monte de 4 étages, redescend de 6 étages, puis remonte de 15 étages et redescend de 8 étages.
À quel étage s'arrête-t-il ?
À quel étage s'arrête-t-il ?
Écrivez la réponse dans la zone colorée.
L'ascenseur s'arrête au e étage.
3 + 4 − 6 + 15 − 8 = 3 + 4 + (−6) + 15 + (−8) = 8
Exercice n°5
Coche la réponse exacte.
a. (−3) + (−4) + 7,2 + (−6,5) =
Cochez la bonne réponse.
| ||
| ||
|
b. (−7) − 5,4 + 8,3 −(−9,4) =
Cochez la bonne réponse.
| ||
| ||
|
a. On regroupe les termes négatifs : (−3) + (−4) + (−6,5) = (−13,5).
Il ne restera plus qu'à ajouter le terme négatif obtenu et le terme positif.
Il ne restera plus qu'à ajouter le terme négatif obtenu et le terme positif.
b. On transforme les soustractions en additions de l'opposé.
(−5,4) devient ainsi + (−5,4) et − (−9,4) s'écrit + 9,4.
(−5,4) devient ainsi + (−5,4) et − (−9,4) s'écrit + 9,4.
Exercice n°6
Coche la réponse exacte.
a. −5 + 2,7 + 9,4 − 2,7 + 5 − 9,4 =
Cochez la bonne réponse.
| ||
| ||
|
b. 6 − 9,5 + 4,3 + 9,5 − 7 =
Cochez la bonne réponse.
| ||
| ||
|
a. La somme de deux nombres opposés est nulle.
−5 + 5 + 2,7 − 2,7 + 9,4 − 9,4 = 0
−5 + 5 + 2,7 − 2,7 + 9,4 − 9,4 = 0

