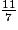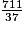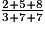Exemple
Calculons : A = 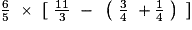 .
.
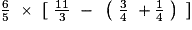 .
.- On effectue d'abord l'addition dans les parenthèses les plus intérieures.
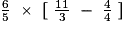 =
= 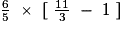
- On fait la soustraction, après avoir réduit au même dénominateur.
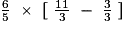 =
= 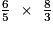
- On multiplie après simplification.
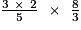 =
= 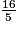
Règle 1
Quand il n'y a pas de parenthèses, la multiplication est prioritaire sur l'addition et la soustraction.
B = 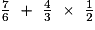 =
= 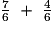 =
= 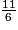
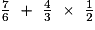 =
= 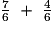 =
= 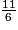
Règle 2
Les opérations au numérateur ou au dénominateur sont prioritaires sur toutes les autres : la barre de fraction équivaut à des parenthèses.
C = 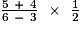 =
= 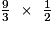 =
= 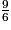
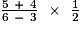 =
= 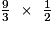 =
= 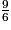
Exercice n°1
Dans chaque série de calculs, quelle opération faut-il faire en priorité ?
Faites glisser les étiquettes dans les zones prévues à cet effet.
la multiplication
la soustraction
l'addition
a. 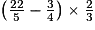 :
:
→
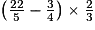 :
:→
imcAnswer1?
b. 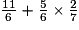 :
:
→
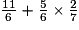 :
:→
imcAnswer2?
c. 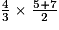 :
:
→
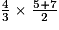 :
:→
imcAnswer3?
a. Les opérations entre parenthèses sont toujours à effectuer en priorité.
b. En l'absence de parenthèses, la multiplication est à effectuer avant l'addition.
c. La barre de fraction équivaut à des parenthèses.
Exercice n°2
Quel est le calcul correspondant à chaque expression ?
a. 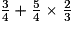 = ?
= ?
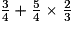 = ?
= ? Cochez la bonne réponse.
| ||
|
b. 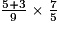 = ?
= ?
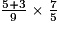 = ?
= ? Cochez la bonne réponse.
| ||
|
a. La multiplication est prioritaire sur l'addition.
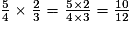
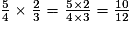
b. La barre de fraction équivaut à des parenthèses.
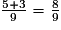 et
et 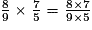
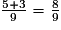 et
et 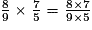
Exercice n°3
Coche la réponse exacte.
a. 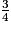 ×
× 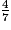 +
+ 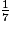 est égal à :
est égal à :
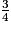 ×
× 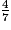 +
+ 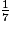 est égal à :
est égal à : Cochez la bonne réponse.
| ||
| ||
|
b. (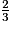 +
+ 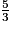 ) (
) (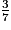 +
+ 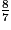 ) est égal à :
) est égal à :
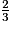 +
+ 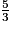 ) (
) (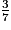 +
+ 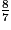 ) est égal à :
) est égal à : Cochez la bonne réponse.
| ||
| ||
|
a. 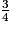 ×
× 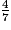 +
+ 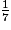 =
= 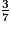 +
+ 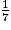
Quand on effectue une suite de calculs avec des fractions, on respecte les priorités opératoires.
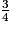 ×
× 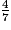 +
+ 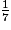 =
= 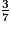 +
+ 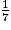
Quand on effectue une suite de calculs avec des fractions, on respecte les priorités opératoires.
b. Il faut ici d'abord effectuer les sommes entre parenthèses.
Exercice n°4
Coche la bonne réponse.
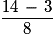 −
− 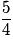 =
= 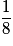
Cochez la bonne réponse.
| ||
|
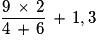 =
= 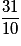
Cochez la bonne réponse.
| ||
|
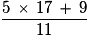 +
+ 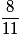 =
= 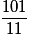
Cochez la bonne réponse.
| ||
|
Les opérations au numérateur ou au dénominateur sont prioritaires sur les autres : une barre de fraction équivaut à des parenthèses.
• 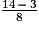 −
− 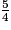 =
= 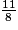 −
− 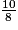 =
= 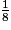
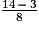 −
− 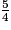 =
= 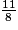 −
− 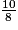 =
= 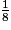
• 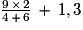 =
= 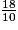 +
+ 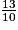 =
= 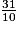
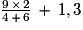 =
= 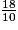 +
+ 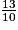 =
= 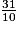
• 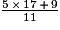 +
+ 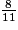 =
= 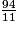 +
+ 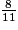 =
= 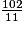
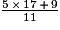 +
+ 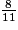 =
= 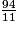 +
+ 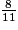 =
= 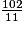
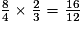
 +
+ 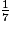
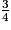 ×
× 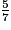
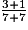
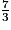 ×
×