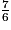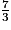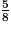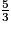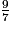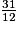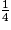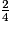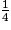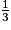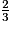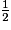1er cas : les fractions ont le même dénominateur.
• Dans le cas d'une addition :
A =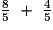 
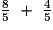
A =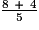 
= 
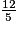← On additionne les numérateurs.
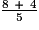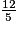= ← On additionne les numérateurs.• Dans le cas d'une soustraction :
B =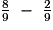 
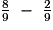
B =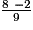 
= 
= 
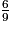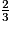← On soustrait les numérateurs.
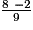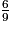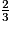= = ← On soustrait les numérateurs.2e cas : il faut parfois modifier les fractions.
+ 
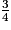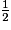: les deux fractions n'ont pas le même dénominateur, on va modifier une fraction.On remarque que 4 = 2 × 2. On va donc multiplier le numérateur et le dénominateur de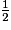 
par 2.
On obtient :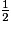
= 
= 
.
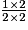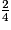Donc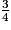
+ 
= 
+ 
= 
.
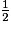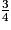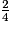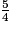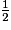par 2.On obtient :
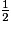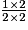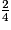= = .Donc
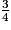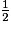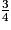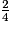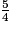+ = + = .Exercice n°1
Coche la réponse exacte.
a.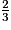 
+ 
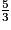est égal à :
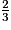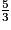+ est égal à : Cochez la bonne réponse.
| ||
| ||
|
b.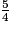 
+ 
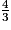est égal à :
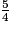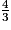+ est égal à : Cochez la bonne réponse.
| ||
| ||
|
Pour additionner des fractions, il faut qu'elles aient le même dénominateur ; il suffit ensuite d'additionner les numérateurs.
Exercice n°2
Coche la réponse exacte.
a. Comment peut-on décomposer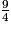 
?
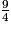? Cochez la bonne réponse.
| ||
| ||
|
b. Comment peut-on décomposer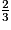 
?
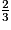? Cochez la bonne réponse.
| ||
| ||
|
a.
 |
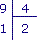La partie entière de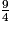 
est 2.
9 = 2 × 4 + 1, d'où :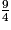
= 
+ 
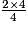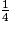= 2 +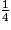 
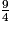est 2.9 = 2 × 4 + 1, d'où :
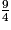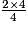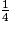= + = 2 + 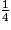b. La fraction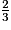 
est plus petite que 1 : sa partie entière est nulle.
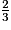est plus petite que 1 : sa partie entière est nulle.
