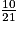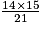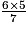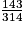Signaler une erreur
Mathématiques - Réviser une notion
Multiplier des fractions
Mathématiques - Réviser une notion
Multiplier des fractions
Imprimer
Mathématiques - Réviser une notion
Multiplier des fractions
Mathématiques - Réviser une notion
Multiplier des fractions
• Pour multiplier des fractions, on multiplie les numérateurs entre eux et les dénominateurs entre eux.
A = 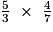 =
= 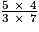 =
= 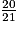
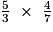 =
= 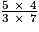 =
= 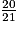
B = 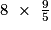 =
= 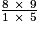 =
= 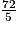
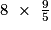 =
= 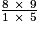 =
= 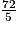
• Il faut souvent simplifier l'écriture avant d'effectuer les multiplications.
C = 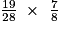 =
= 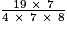 =
= 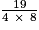 =
= 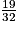
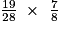 =
= 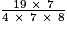 =
= 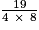 =
= 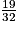
• Remarques :
– Calculer « les trois quarts des quatre cinquièmes » revient à faire la multiplication :
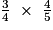 =
= 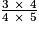 =
= 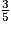
– De même, calculer « 75 % des trois quarts » revient à faire la multiplication :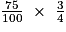 =
= 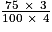 =
= 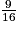
– Calculer « les trois quarts des quatre cinquièmes » revient à faire la multiplication :
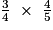 =
= 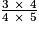 =
= 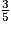
– De même, calculer « 75 % des trois quarts » revient à faire la multiplication :
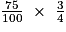 =
= 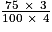 =
= 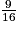
Exercice n°1
Coche la réponse exacte.
a. 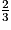 ×
× 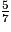 est égal à :
est égal à :
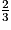 ×
× 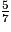 est égal à :
est égal à : Cochez la bonne réponse.
| ||
| ||
|
b. 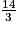 ×
× 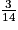 est égal à :
est égal à :
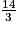 ×
× 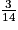 est égal à :
est égal à : Cochez la bonne réponse.
| ||
| ||
|
Pour multiplier des fractions on multiplie les numérateurs entre eux et les dénominateurs entre eux. On simplifie le résultat si nécessaire.
Exercice n°2
Quelles sont les fractions égales au produit 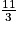 ×
× 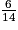 ×
× 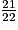 ?
?
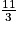 ×
× 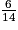 ×
× 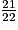 ?
? Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
Multiplie les numérateurs, puis les dénominateurs.
Il faut penser à simplifier avant d'effectuer les multiplications. 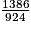 est simplifiable
est simplifiable
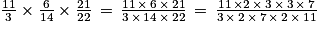 =
= 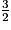 .
.
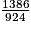 est simplifiable
est simplifiable 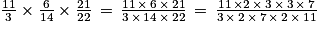 =
= 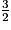 .
.
Signaler une erreur
Mathématiques - Réviser une notion
Multiplier des fractions
Mathématiques - Réviser une notion
Multiplier des fractions
Imprimer
Mathématiques - Réviser une notion
Multiplier des fractions
Mathématiques - Réviser une notion
Multiplier des fractions