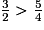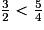• Rappel :
 |
• Si deux fractions ont le même dénominateur, la plus grande est celle qui a le plus grand numérateur.
Ainsi 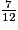 et
et 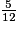 ont le même dénominateur et 7 > 5, donc
ont le même dénominateur et 7 > 5, donc 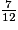 >
> 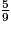 .
.
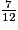 et
et 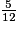 ont le même dénominateur et 7 > 5, donc
ont le même dénominateur et 7 > 5, donc 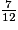 >
> 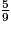 .
.• Si deux fractions ont le même numérateur, la plus grande est celle qui a le plus petit dénominateur.
En effet, plus le dénominateur est petit, moins on a fait de parts, donc plus grosses sont les parts.
Ainsi, 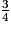 et
et 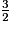 ont le même numérateur et 2 < 4, donc
ont le même numérateur et 2 < 4, donc 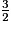 >
> 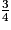 .
.
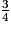 et
et 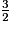 ont le même numérateur et 2 < 4, donc
ont le même numérateur et 2 < 4, donc 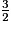 >
> 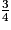 .
.Exercice n°1
Complète avec le signe < ou >.
Faites glisser les étiquettes dans les zones prévues à cet effet.
<
>
a. 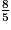
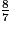 car les deux fractions ont le même numérateur et 5
car les deux fractions ont le même numérateur et 5
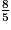
imcAnswer1|imcAnswer3|imcAnswer4|imcAnswer6?
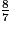 car les deux fractions ont le même numérateur et 5
car les deux fractions ont le même numérateur et 5 imcAnswer2|imcAnswer5?
7. b. 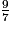
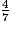 car les deux fractions ont le même dénominateur et 9
car les deux fractions ont le même dénominateur et 9
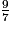
imcAnswer1|imcAnswer3|imcAnswer4|imcAnswer6?
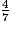 car les deux fractions ont le même dénominateur et 9
car les deux fractions ont le même dénominateur et 9 imcAnswer1|imcAnswer3|imcAnswer4|imcAnswer6?
4. c. 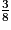
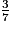 car les deux fractions ont le même numérateur et 8
car les deux fractions ont le même numérateur et 8
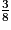
imcAnswer2|imcAnswer5?
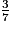 car les deux fractions ont le même numérateur et 8
car les deux fractions ont le même numérateur et 8 imcAnswer1|imcAnswer3|imcAnswer4|imcAnswer6?
7.Des fractions de même numérateur sont rangées dans l'ordre inverse de leurs dénominateurs.
5 < 7 donc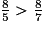 .
.
8 > 7 donc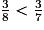 .
.
5 < 7 donc
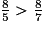 .
.8 > 7 donc
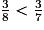 .
.Exercice n°2
Complète avec le signe < ou >.
Faites glisser les étiquettes dans les zones prévues à cet effet.
>
<
a. 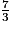
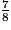
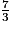
imcAnswer7|imcAnswer10?
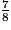
b. 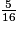
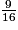
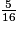
imcAnswer8|imcAnswer9?
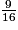
c. 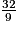
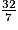
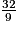
imcAnswer8|imcAnswer9?
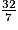
d. 
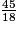

imcAnswer7|imcAnswer10?
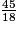
a. 3 < 8 donc 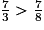 .
.
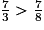 .
. b. 5 < 9 donc 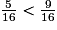 .
.
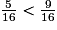 .
. c. 9 > 7 donc 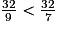 .
.
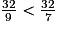 .
.Exercice n°3
Complète avec le signe < ou >.
Faites glisser les étiquettes dans les zones prévues à cet effet.
<
>
a. 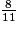
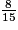
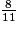
imcAnswer11|imcAnswer12?
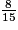
b. 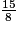
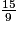
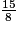
imcAnswer11|imcAnswer12?
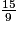
c. 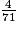
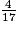
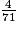
imcAnswer13|imcAnswer14?
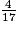
d. 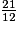
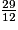
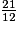
imcAnswer13|imcAnswer14?
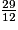
• Si deux fractions ont le même numérateur, la plus grande est celle qui a le dénominateur le plus petit.
• Si deux fractions ont le même dénominateur, la plus grande est celle qui a le numérateur le plus grand.
a. 11 < 15 donc 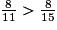 .
.
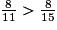 .
. b. 8 < 9 donc 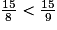 .
.
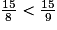 .
. c. 71 > 17 donc 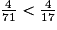 .
.
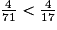 .
. d. 21 < 29 donc 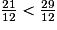 .
.
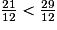 .
.Exercice n°4
Quelles inégalités sont vraies ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
|
• Quand deux fractions ont le même dénominateur, la plus grande est celle qui a le numérateur le plus grand.
• Quand deux fractions ont le même numérateur, la plus grande est celle qui a le dénominateur le plus petit.
Exercice n°5
Fais les exercices dans l'ordre proposé.
a. Parmi ces fractions, lesquelles sont plus petites que 1 ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
| ||
| ||
|
b. Classe dans l'ordre croissant ces fractions (toutes plus petites que 1).
Faites glisser les étiquettes dans les zones prévues à cet effet.
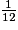
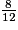
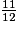
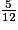
imcAnswer29?
< imcAnswer30?
< imcAnswer31?
< imcAnswer32?
c. Classe dans l'ordre croissant ces fractions (toutes plus grandes que 1).
Faites glisser les étiquettes dans les zones prévues à cet effet.
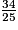
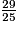
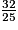
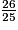
imcAnswer33?
< imcAnswer34?
< imcAnswer35?
< imcAnswer36?
a. Une fraction est plus petite que 1 si son numérateur est plus petit que son dénominateur.
2 et 3. Ici, toutes les fractions plus petites que 1 ont le même dénominateur. Pour les ranger dans l'ordre croissant, il suffit de ranger leurs numérateurs dans l'ordre croissant. Il en est de même pour les fractions plus grandes que 1.
Exercice n°6
Coche la réponse exacte.
a. Pour comparer 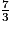 et
et 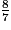 :
:
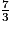 et
et 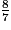 :
: Cochez la bonne réponse.
| ||
| ||
|
b. Quelle comparaison est vraie ?
Cochez la bonne réponse.
| ||
| ||
|
b. Pour comparer 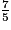 et
et 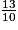 , on réduit les fractions au même dénominateur :
, on réduit les fractions au même dénominateur :
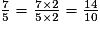
On compare ensuite les numérateurs (14 > 13) et on en déduit :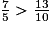 .
.
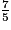 et
et 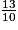 , on réduit les fractions au même dénominateur :
, on réduit les fractions au même dénominateur :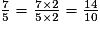
On compare ensuite les numérateurs (14 > 13) et on en déduit :
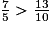 .
.Exercice n°7
On veut comparer 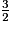 et
et 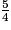 . Lequel des trois raisonnements suivants est faux ?
. Lequel des trois raisonnements suivants est faux ?
Coche la réponse exacte.
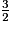 et
et 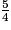 . Lequel des trois raisonnements suivants est faux ?
. Lequel des trois raisonnements suivants est faux ?Coche la réponse exacte.
Cochez la bonne réponse.
| ||
| ||
|
Attention, on ne peut comparer des fractions que si elles ont le même numérateur ou le même dénominateur.
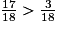
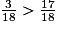
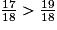
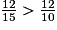
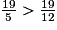
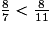
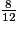
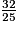
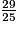
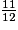
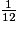
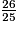
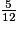
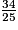
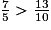
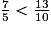
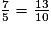
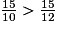 donc
donc 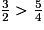
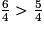 donc
donc