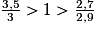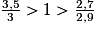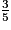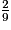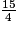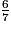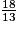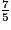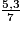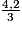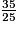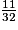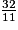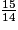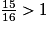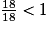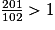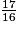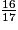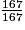• On veut comparer à l'unité les fractions : 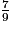 ;
; 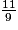 ;
; 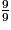 .
.
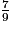 ;
; 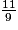 ;
; 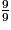 .
.Pour cela, on compare leur numérateur à leur dénominateur.
7 < 9 donc 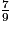 < 1.
< 1.
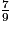 < 1.
< 1.11 > 9 donc 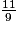 > 1.
> 1.
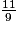 > 1.
> 1.9 = 9 donc 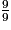 = 1.
= 1.
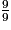 = 1.
= 1.• On peut aussi calculer la valeur décimale de la fraction.
Exemple : 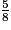 = 0,625 donc
= 0,625 donc 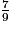 < 1.
< 1.
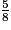 = 0,625 donc
= 0,625 donc 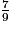 < 1.
< 1.• Quand on range des fractions, on peut commencer par comparer chacune d'elles à l'unité.
Exemple : On veut ranger dans l'ordre croissant : 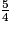 ;
; 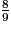 ;
; 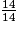 .
.
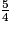 ;
; 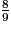 ;
; 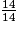 .
.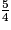 > 1 ;
> 1 ; 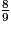 < 1 ;
< 1 ; 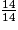 = 1.
= 1.Donc : 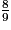 <
< 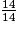 <
< 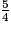 .
.
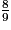 <
< 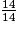 <
< 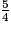 .
.Exercice n°1
Complète avec plus grand(e), plus petit(e) ou égal(e).
Écrivez les réponses dans les zones colorées.
1. Dans 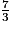 , le numérateur est que le dénominateur ; la fraction est que 1.
, le numérateur est que le dénominateur ; la fraction est que 1.
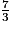 , le numérateur est que le dénominateur ; la fraction est que 1.
, le numérateur est que le dénominateur ; la fraction est que 1. 2. Dans 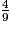 , le numérateur est que le dénominateur ; la fraction est que 1.
, le numérateur est que le dénominateur ; la fraction est que 1.
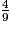 , le numérateur est que le dénominateur ; la fraction est que 1.
, le numérateur est que le dénominateur ; la fraction est que 1. 3. Dans 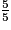 , le numérateur est au dénominateur ; la fraction est à 1.
, le numérateur est au dénominateur ; la fraction est à 1.
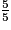 , le numérateur est au dénominateur ; la fraction est à 1.
, le numérateur est au dénominateur ; la fraction est à 1. 1. 7 > 3
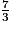 est donc plus grand que 1.
est donc plus grand que 1.
7 ÷ 3 = 2,33333…
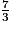 est donc plus grand que 1.
est donc plus grand que 1.7 ÷ 3 = 2,33333…
2. 4 < 9
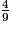 est donc plus petit que 1.
est donc plus petit que 1.
4 ÷ 9 = 0,44444…
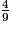 est donc plus petit que 1.
est donc plus petit que 1.4 ÷ 9 = 0,44444…
Exercice n°2
Quelles sont les fractions inférieures à 1 ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
|
• Il faut comparer le numérateur (nombre du « haut ») et le dénominateur (nombre du « bas »).
• La fraction est plus petite que 1 si le numérateur est plus petit que le dénominateur.
Exercice n°3
Coche les réponses exactes.
a. Quelle fraction est plus petite que 1 ?
Cochez la bonne réponse.
| ||
| ||
|
b. Quelle inégalité est vraie ?
Cochez la bonne réponse.
| ||
| ||
|
c. Quelle fraction est plus grande que 1 ?
Cochez la bonne réponse.
| ||
| ||
|
• Une fraction est inférieure à 1 si le numérateur est plus petit que le dénominateur.
• Une fraction est supérieure à 1 si le numérateur est plus grand que le dénominateur.
Exercice n°4
Complète par le signe qui convient.
Faites glisser les étiquettes dans les zones prévues à cet effet.
<
>
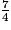
imcAnswer19|imcAnswer21?
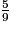
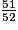
imcAnswer20?
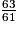
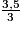
imcAnswer19|imcAnswer21?
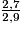
Compare chacune des fractions au nombre 1.
• 7 > 4 donc 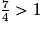 et 5 < 9 donc
et 5 < 9 donc 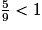 . On obtient
. On obtient 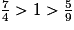 .
.
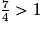 et 5 < 9 donc
et 5 < 9 donc 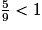 . On obtient
. On obtient 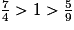 .
.• 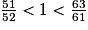
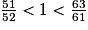
•