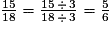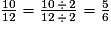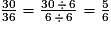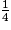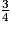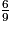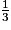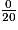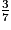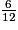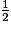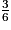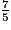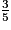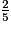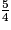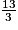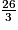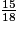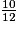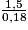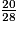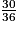• Pour simplifier une fraction, il faut trouver un diviseur commun au numérateur et au dénominateur.
Exemple : on veut simplifier 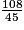 .
.
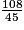 .
.- On remarque que 108 et 45 sont divisibles par 9.
- On écrit :
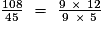
- On simplifie par 9 :
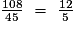 .
.
• On peut parfois effectuer plusieurs simplifications.
Exemple : on veut simplifier 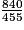 .
.
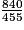 .
.- On cherche les diviseurs :
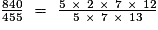
- On simplifie par 5 et par 7 :
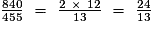
Exercice n°1
Coche les réponses exactes.
a. 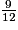 est égal à :
est égal à :
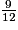 est égal à :
est égal à : Cochez la bonne réponse.
| ||
| ||
|
b. 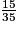 est égal à :
est égal à :
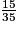 est égal à :
est égal à : Cochez la bonne réponse.
| ||
| ||
|
c. La fraction irréductible égale à 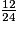 est :
est :
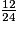 est :
est : Cochez la bonne réponse.
| ||
| ||
|
• a.
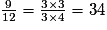
On a simplifié par 3.
• b.
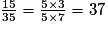
On a simplifié par 5.
• c.
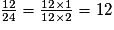
On a simplifié par 12.
Exercice n°2
On veut simplifier chaque fraction.
Sélectionne la fraction simplifiée qui convient.
Sélectionne la fraction simplifiée qui convient.
a. 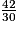
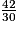
Cochez la bonne réponse.
| ||
|
b. 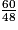
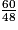
Cochez la bonne réponse.
| ||
|
c. 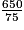
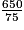
Cochez la bonne réponse.
| ||
|
a. 42 = 6 × 7
30 = 6 × 5
30 = 6 × 5
b. 60 = 6 × 10 = 6 × 2 × 5
48 = 6 × 8 = 6 × 2 × 4
48 = 6 × 8 = 6 × 2 × 4
c. 650 = 10 × 65 = 2 × 5 × 5 × 13
75 = 3 × 25 = 3 × 5 × 5
75 = 3 × 25 = 3 × 5 × 5
Exercice n°3
Quelles sont les fractions égales à 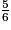 ?
?
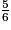 ?
? Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
|
Le quotient de deux nombres ne change pas si on divise (ou on multiplie) son numérateur et son dénominateur par un même nombre.