Si l'on connaît l'aire et l'une des longueurs de certains quadrilatères (rectangles et trapèzes), on peut retrouver l'autre longueur ou la hauteur par une division.
Calcul d'une longueur dans un rectangle
L'aire d'une plaque rectangulaire est de 3,375 m2, sa largeur mesure 45 cm.
Quelle est sa longueur ?
- On doit convertir l'aire en cm2 : 3,375 m2 = 33 750 cm2.
- La longueur L en cm est alors solution de l'équation : 45 × L = 33 750.
L = 33 750 ÷ 45 = 750
La longueur de la plaque est : 7,5 m.
Calcul d'une hauteur dans un triangle
Un côté d'un triangle EFG mesure 80 mm.
Quelle est la mesure h de la hauteur relative à ce côté si l'aire de ce triangle est 280 mm² ?
- Utilisons la formule de l'aire d'un triangle ; h est la seule inconnue et on a :
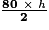= 280. - On en déduit que : 80 × h = 560.
La hauteur mesure en mm : 560 ÷ 80 = 7.
Exercice n°1
 |
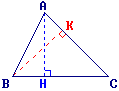Le triangle ABC possède les propriétés suivantes :
[AH]
[BC] et [BK] 
[AC] ; BC = 6 cm ; AC = 5 cm ; AH = 4 cm.
Calcule l'aire du triangle et déduis la hauteur BK.
[AH]
[BC] et [BK] [AC] ; BC = 6 cm ; AC = 5 cm ; AH = 4 cm.Calcule l'aire du triangle et déduis la hauteur BK.
Écrivez les réponses dans les zones colorées.
1. L'aire du triangle ABC est cm2.
2. La hauteur BK mesure cm.
1. [AH] est la hauteur relative au côté [BC].
Aire de ABC = AH × BC ÷ 2 = 12.
Aire de ABC = AH × BC ÷ 2 = 12.
2. [BK] est la hauteur relative au côté [AC].
Aire de ABC = BK × AC ÷ 2
12 = BK × 5 ÷ 2
Donc BK × 5 = 12 × 2 = 24 et BK = 24 ÷ 5 = 4,8.
Aire de ABC = BK × AC ÷ 2
12 = BK × 5 ÷ 2
Donc BK × 5 = 12 × 2 = 24 et BK = 24 ÷ 5 = 4,8.
Exercice n°2
 |
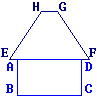Le rectangle ABCD et le trapèze EFGH ont la même aire.
Les mesures sont :
AD = 8 m ; AB = 3 m ; EF = 10 m ; GH = 2 m.
Calcule l'aire du rectangle et déduis la hauteur du trapèze.
Les mesures sont :
AD = 8 m ; AB = 3 m ; EF = 10 m ; GH = 2 m.
Calcule l'aire du rectangle et déduis la hauteur du trapèze.
Écrivez les réponses dans les zones colorées.
1. L'aire du rectangle est m2.
2. La hauteur du trapèze est m.
1. Aire de ABCD = 3 × 8 = 24.
2. Aire de EFGH = (EF + HG) × h ÷ 2 avec h, la hauteur du trapèze.
Donc 24 = (10 + 2) × h ÷ 2
soit 24 = 12 × h ÷ 2.
On en déduit que :
12 × h = 24 × 2 = 48
donc h = 48 ÷ 12 = 4.
Donc 24 = (10 + 2) × h ÷ 2
soit 24 = 12 × h ÷ 2.
On en déduit que :
12 × h = 24 × 2 = 48
donc h = 48 ÷ 12 = 4.
Exercice n°3
Coche la bonne réponse.
a. L'aire d'un triangle est 36 cm2. Un de ses côtés mesure 8 cm. La hauteur relative à ce côté mesure :
Cochez la bonne réponse.
| ||
| ||
|
b. Un carré a pour aire 36 cm2 ; son côté mesure :
Cochez la bonne réponse.
| ||
| ||
|
a. On obtient la mesure de la hauteur en divisant le double de l'aire du triangle ((2 × 36) cm2) par la mesure du côté (8 cm).
b. Remarque que 6 × 6 = 36.
Exercice n°4
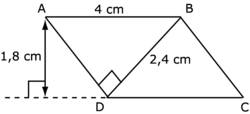
Que vaut la longueur AD ?
 |
Cochez la bonne réponse.
| ||
| ||
|
Calcule l'aire du parallélogramme en utilisant la base AB.
• L'aire du parallélogramme ABCD est égale à AB × 1,8 = 4 × 1,8 = 7,2 cm2.
• L'aire du parallélogramme ABCD est aussi égale à BD × AD = 2,4 × AD.
• On obtient 2,4 × AD = 7,2 soit AD = 7,2 ÷ 2,4 = 3 cm.
