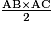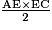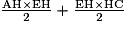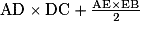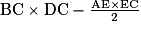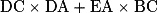Pour calculer l'aire d'un polygone, on peut le partager en triangles ou en quadrilatères particuliers.
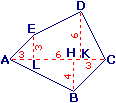
On veut calculer l'aire du pentagone ABCDE
 |
On a :
AL = 3 ; LK = 6 ; KC = 3 ;
BH = 4 ; DK = 6 ; EL = 3.
AL = 3 ; LK = 6 ; KC = 3 ;
BH = 4 ; DK = 6 ; EL = 3.
ABCDE se décompose en 3 triangles et 1 trapèze :
aire de ALE : (3 × 3) ÷ 2 = 4,5 ;
aire de CKD : (3 × 6) ÷ 2 = 9 ;
aire de ABC : (3 + 6 + 3) × 4 ÷ 2 = 24 ;
aire de DKLE : (3 + 6) × 6 ÷ 2 = 27.
aire de ALE : (3 × 3) ÷ 2 = 4,5 ;
aire de CKD : (3 × 6) ÷ 2 = 9 ;
aire de ABC : (3 + 6 + 3) × 4 ÷ 2 = 24 ;
aire de DKLE : (3 + 6) × 6 ÷ 2 = 27.
On en déduit :
aire de ABCDE : 4,5 + 9 + 24 + 27 = 64,5.
aire de ABCDE : 4,5 + 9 + 24 + 27 = 64,5.
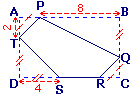
On veut calculer l'aire du pentagone PQRST
 |
On a :
AP = AT = CQ = CR = 2
DS = DT = BQ = 4
PB = 8
AP = AT = CQ = CR = 2
DS = DT = BQ = 4
PB = 8
On sait que ABCD a pour aire 60.
Les triangles APT, PBQ, QCR, SDT ont pour aires respectives : 2, 16, 2 et 8.
L'aire de PQRST est la différence :
60 – (2 + 16 + 2 + 8) = 60 – 28 = 32.
60 – (2 + 16 + 2 + 8) = 60 – 28 = 32.
Exercice n°1
 |
On sait que :
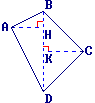
(AH)
(BD) et (CK) 
(BD) ; BH = 2 ; HK = 3 ; KD = 5 ; AH = 4 ; CK = 5.
Calcule l'aire du quadrilatère ABCD.
(AH)
(BD) et (CK) (BD) ; BH = 2 ; HK = 3 ; KD = 5 ; AH = 4 ; CK = 5.Calcule l'aire du quadrilatère ABCD.
Écrivez les réponses dans les zones colorées.
1. Aire de BAD = .
2. Aire de BCD = .
3. Aire totale de ABCD = .
1. Aire de BAD = AH × BD ÷ 2 = 4 × 10 ÷ 2 = 20.
2. Aire de BCD = CK × BD ÷ 2 = 5 × 10 ÷ 2 = 25.
3. Aire de ABCD = 20 + 25 = 45.
Exercice n°2
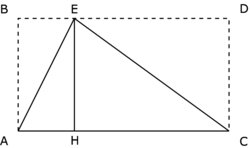
Quelle est l'aire du triangle AEC ci-dessous ?
 |
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
|
Le triangle AEC est partagé en deux triangles rectangles.
• Le triangle AEC représente la moitié du rectangle ABDC. L'aire du rectangle ABDC est AB × AC, donc l'aire du triangle AEC est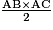 
.
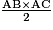.• Le triangle AEC est partagé en deux triangles rectangles AHE et EHC. L'aire du triangle AEC est égale à la somme des aires des deux triangles AHE et EHC, soit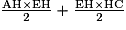 
.
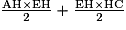.Exercice n°3
 |
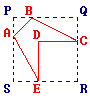Tu sais que :
- PQRS est un carré de côté 8 ;
- CRED est un carré de côté 5 ;
- PA = PB = 2.
Calcule l'aire du polygone ABCDE en suivant les étapes proposées.
Écrivez les réponses dans les zones colorées.
a. Aire de PQRS :
b. Aire de CRED :
c. Aire de PBA :
d. Aire de QCB :
e. Aire de ASE :
f. Aire de ABCDE :
d. QC = QR − CR = 8 − 5 = 3
QB = PQ − PB = 8 − 2 = 6
Aire de QCB = 3 × 6 ÷ 2 = 9
QB = PQ − PB = 8 − 2 = 6
Aire de QCB = 3 × 6 ÷ 2 = 9
e. AS = PS − PA = 8 − 2 = 6
SE = SR − ER = 8 − 5 = 3
Aire de ASE = 6 × 3 ÷ 2 = 9
SE = SR − ER = 8 − 5 = 3
Aire de ASE = 6 × 3 ÷ 2 = 9
f. Aire de ABCDE = 64 − 25 − 2 − 9 − 9 = 19
Exercice n°4
Quelle est l'aire de la figure ci-dessous ?
 |
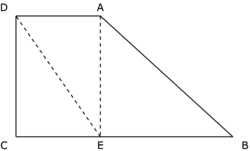Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
|
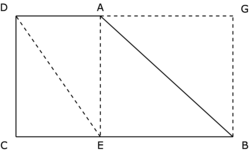
Partage la figure en un rectangle et un triangle.
• L'aire de la figure est égale à : Aire du rectangle ADCE + Aire du triangle rectangle AEB.
• L'aire de la figure est aussi égale à : Aire du rectangle DCBG − Aire du triangle rectangle AGB.
 |
