L'aire d'un disque de rayon R est égale à : π × R × R.
Aire d'un disque :
Quelle est l'aire d'un disque de diamètre 10 cm ?
Réponse : le rayon d'un disque est la moitié de son diamètre, donc R = 5 cm.
L'aire du disque, en cm2, est :
3,14 × 5 × 5 = 78,5 car 
3,14.
3,14.Aire d'un secteur circulaire :
On découpe dans le disque précédent un secteur circulaire mesurant 72°.
 |
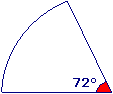Quelle est l'aire de ce secteur ?
Réponse : puisqu'un secteur plein mesure 360°, un secteur de 72°correspond à la fraction du disque.
Son aire est égale, en cm2, à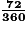 
de l'aire du disque : 
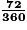× 78,5 = 15,7.
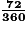de l'aire du disque : 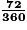× 78,5 = 15,7.Exercice n°1
Complète les réponses en prenant 3,14 pour π.
Écrivez les réponses dans les zones colorées.
1. Rayon du disque : 3 cm
Diamètre du disque : cm
Aire du disque : cm2
Diamètre du disque : cm
Aire du disque : cm2
2. Rayon du disque : cm
Diamètre du disque : 8 cm
Aire du disque : cm2
Diamètre du disque : 8 cm
Aire du disque : cm2
3. Rayon du disque : cm
Diamètre du disque : 13 cm
Aire du disque : cm2
Diamètre du disque : 13 cm
Aire du disque : cm2
4. Rayon du disque : cm
Diamètre du disque : cm
Aire du disque : 314 cm2
Diamètre du disque : cm
Aire du disque : 314 cm2
1. A = 3,14 × 32 = 28,26 cm2.
2. A = 3,14 × 42 = 50,24 cm2.
3. A = 3,14 × 6,52 = 132,665 cm2.
4. 314 = 3,14 × R2
R2 =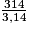
= 100.
Or 100 = 10 × 10 donc R = 10 cm.
R2 =
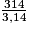= 100. Or 100 = 10 × 10 donc R = 10 cm.
Exercice n°2
Coche les réponses exactes.
1. Un disque de rayon R a pour aire :
Cochez la bonne réponse.
| ||
| ||
|
2. Un disque de rayon 8 cm a pour aire :
Cochez la bonne réponse.
| ||
| ||
|
Attention : π × R × 2 est différent de π × R × R !
Exercice n°3
On considère un disque de rayon 5 cm.
Calcule les aires suivantes.
Calcule les aires suivantes.
Écrivez les réponses dans les zones colorées.
1. Quelle est l'aire du disque ? (Utilise la touche π de la calculatrice et arrondis au dixième.)
Réponse : cm2.
Réponse : cm2.
2. Quelle est l'aire d'un quart de ce disque ? (Arrondis au dixième.)
Réponse : cm2.
Réponse : cm2.
3. Quelle est l'aire d'un secteur circulaire de 25° découpé dans ce disque ? (Arrondis au dixième.)
Réponse : cm2.
Réponse : cm2.
1. Aire du disque :
5 × 5 × 3,14 = 78,5.
5 × 5 × 3,14 = 78,5.
2. Aire du quart de disque :
78,5 ÷ 4 = 19,6.
78,5 ÷ 4 = 19,6.
3. Le secteur de 25° représente 25/360 du disque :
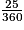× 78,5 = 5,5.
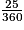× 78,5 = 5,5.Exercice n°4
Un disque a un rayon de 12 cm.
Complète les calculs d'aire suivants.
Complète les calculs d'aire suivants.
Écrivez les réponses dans les zones colorées.
a. L'aire du disque est × 3,14 cm2.
b. Si on divisait le rayon du disque par 6, l'aire du disque réduit serait : × 3,14 cm2.
c. L'aire d'un secteur circulaire de 60° et de rayon 12 cm est : × 3,14 cm2.
a. Aire = 12 × 12 × 3,14 = 144 × 3,14
b. 12 ÷ 6 = 2
Aire = 2 × 2 × 3,14 = 4 × 3,14
Aire = 2 × 2 × 3,14 = 4 × 3,14
c. 60 = 360 ÷ 6
Aire = (144 × 3,14) ÷ 6 = 24 × 3,14
Aire = (144 × 3,14) ÷ 6 = 24 × 3,14
Exercice n°5
Un disque a un rayon de 12 cm.
Complète les phrases suivantes.
Complète les phrases suivantes.
Écrivez les réponses dans les zones colorées.
a. L'aire de ce disque est × 3,14.
b. L'aire du quart de ce disque est × 3,14.
c. Si on divise le rayon de ce disque par 6, l'aire devient × 3,14.
a. L'aire de ce disque est 12 × 12 × soit 144 × 3,14.
b. L'aire du quart de ce disque est l'aire du disque divisée par 4, soit 36 × 3,14.
c. Si on divise le rayon de ce disque par 6, le rayon devient 2 cm et l'aire devient 4 × 3,14.
Exercice n°6
Complète les phrases suivantes.
Un disque a pour diamètre 10 cm.
Écrivez les réponses dans les zones colorées.
L'aire de ce disque est : ×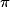 
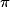cm2.
cm2.Le cinquième de ce disque a pour aire : ×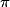 
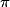cm2.
cm2.Si on divise le rayon de ce disque par 10, l'aire devient : ×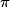 
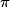cm2.
cm2.Le rayon est égal à la moitié du diamètre.
• Le rayon est égal à 10 ÷ 2 = 5 cm. L'aire est égale à 52 × π = 25 × π cm2.
• On a : (25 × π) ÷ 5 = 5 × π cm2.
• Le rayon est égal à 5 ÷ 10 = 0,5 cm. L'aire est égale à 0,52 × π = 0,25 × π cm2.
