Signaler une erreur
Mathématiques - Réviser une notion
Réduire des fractions au même dénominateur
Mathématiques - Réviser une notion
Réduire des fractions au même dénominateur
Imprimer
Mathématiques - Réviser une notion
Réduire des fractions au même dénominateur
Mathématiques - Réviser une notion
Réduire des fractions au même dénominateur
Pour réduire des fractions au même dénominateur, il faut trouver le plus petit multiple commun aux dénominateurs.
On distingue plusieurs cas :
• L'un des dénominateurs est multiple de l'autre.
Exemple :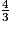 et
et 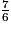 ; 6 = 3 × 2.
; 6 = 3 × 2.
6 est le dénominateur commun.
On transforme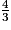 et
et 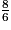 .
.
Exemple :
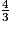 et
et 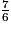 ; 6 = 3 × 2.
; 6 = 3 × 2.6 est le dénominateur commun.
On transforme
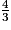 et
et 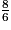 .
.• L'un des nombres est un entier.
Exemple : 4 et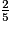 .
.
5 est le dénominateur commun.
On écrit :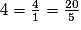 .
.
Exemple : 4 et
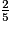 .
.5 est le dénominateur commun.
On écrit :
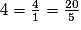 .
.• Un multiple commun aux deux dénominateurs se trouve dans les tables de multiplication.
Exemple :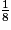 et
et 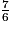 .
.
8 × 3 = 24 et 6 × 4 = 24.
Le dénominateur commun est donc 24.
On transforme :
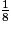 en
en 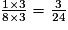 .
.
et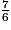 en
en 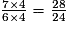 .
.
Exemple :
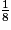 et
et 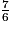 .
.8 × 3 = 24 et 6 × 4 = 24.
Le dénominateur commun est donc 24.
On transforme :
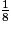 en
en 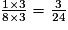 .
.et
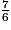 en
en 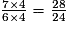 .
.• Les dénominateurs sont quelconques : le dénominateur commun est le produit des deux.
Exercice n°1
Coche le plus petit des dénominateurs communs.
a. 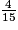 et
et 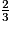
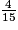 et
et 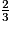
Cochez la bonne réponse.
| ||
| ||
|
b. 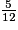 et
et 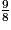
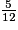 et
et 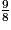
Cochez la bonne réponse.
| ||
| ||
|
c. 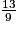 et
et 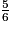
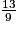 et
et 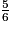
Cochez la bonne réponse.
| ||
| ||
|
a. 15 = 3 × 5.
b. 24 = 12 × 2 et 24 = 8 × 3.
c. 18 = 9 × 2 et 18 = 6 × 3.
Signaler une erreur
Mathématiques - Réviser une notion
Réduire des fractions au même dénominateur
Mathématiques - Réviser une notion
Réduire des fractions au même dénominateur
Imprimer
Mathématiques - Réviser une notion
Réduire des fractions au même dénominateur
Mathématiques - Réviser une notion
Réduire des fractions au même dénominateur

