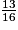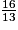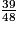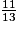Signaler une erreur
Mathématiques - Réviser une notion
Additionner, soustraire, multiplier des fractions
Mathématiques - Réviser une notion
Additionner, soustraire, multiplier des fractions
Imprimer
Mathématiques - Réviser une notion
Additionner, soustraire, multiplier des fractions
Mathématiques - Réviser une notion
Additionner, soustraire, multiplier des fractions
Addition et soustraction de fractions
On ne peut additionner ou soustraire des fractions que si elles ont le même dénominateur.
• Calculons : 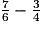 .
.
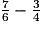 .
.• On réduit les fractions au même dénominateur : ici, 12.
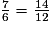 et
et 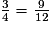 .
.
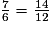 et
et 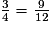 .
.• On effectue la différence :
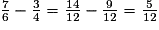 .
.
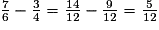 .
.Multiplication de fractions
Pour multiplier des fractions, on multiplie les numérateurs entre eux et les dénominateurs entre eux.
Attention aux simplifications possibles en cours de calcul !
• Calculons : 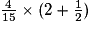 .
.
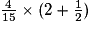 .
.• On fait d'abord la somme entre parenthèses :
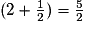 .
.
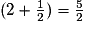 .
.• On effectue la multiplication après avoir simplifié :
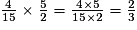 .
.
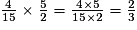 .
.Exercice n°1
Soit A = 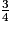 ×(2 −
×(2 − 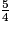 +
+ 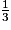 ).
).
Quelle est la valeur simplifiée de A ?
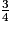 ×(2 −
×(2 − 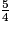 +
+ 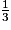 ).
).Quelle est la valeur simplifiée de A ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Commence par calculer l'expression entre parenthèses. Tu peux prendre 12 pour dénominateur commun.
Commence par calculer l'expression entre parenthèses.
A =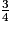 × (2 −
× (2 − 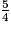 +
+ 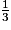 )
)
A =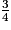 × (
× (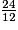 −
− 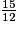 +
+ 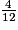 )
)
A =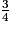 × (
× (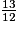 )
)
A =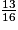
A =
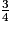 × (2 −
× (2 − 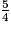 +
+ 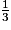 )
)A =
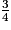 × (
× (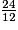 −
− 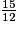 +
+ 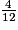 )
)A =
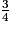 × (
× (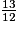 )
)A =
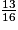
Signaler une erreur
Mathématiques - Réviser une notion
Additionner, soustraire, multiplier des fractions
Mathématiques - Réviser une notion
Additionner, soustraire, multiplier des fractions
Imprimer
Mathématiques - Réviser une notion
Additionner, soustraire, multiplier des fractions
Mathématiques - Réviser une notion
Additionner, soustraire, multiplier des fractions