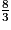Il existe deux manières de ranger plusieurs fractions :
- par ordre croissant, c'est-à-dire de la plus petite à la grande ;
- par ordre décroissant, c'est-à-dire de la plus grande à la plus petite.
On veut ranger dans l'ordre croissant les fractions suivantes :
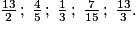
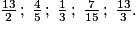
• On réunit les fractions inférieures à 1 (celles dont le numérateur est plus petit que le dénominateur) :
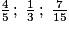
puis les fractions supérieures à 1 (celles dont le numérateur est plus grand que le dénominateur) :
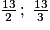 .
.
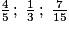
puis les fractions supérieures à 1 (celles dont le numérateur est plus grand que le dénominateur) :
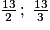 .
.• On classe les fractions inférieures à 1 en les réduisant au même dénominateur 15.
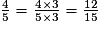
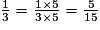
On a donc :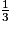 <
< 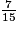 <
< 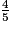 .
.
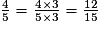
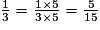
On a donc :
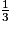 <
< 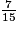 <
< 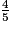 .
.• On classe les deux fractions supérieures à 1.
Elles ont le même numérateur 13, et 3 > 2, donc :
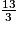 <
< 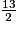 .
.
Elles ont le même numérateur 13, et 3 > 2, donc :
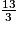 <
< 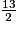 .
.• On réunit les deux classements :
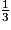 <
< 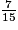 <
< 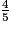 <
< 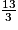 <
< 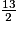 .
.
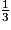 <
< 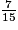 <
< 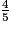 <
< 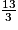 <
< 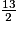 .
.Exercice n°1
On considère les fractions suivantes : 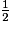 ;
; 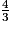 ;
; 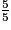 ;
; 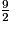 ;
; 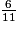 ;
; 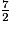 .
.
Dans la liste des fractions ci-dessous, combien y en a-t-il qui sont strictement supérieures à 1 ?
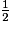 ;
; 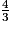 ;
; 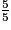 ;
; 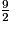 ;
; 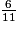 ;
; 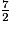 .
.Dans la liste des fractions ci-dessous, combien y en a-t-il qui sont strictement supérieures à 1 ?
Cochez la bonne réponse.
| ||
| ||
| ||
| ||
| ||
| ||
|
Les fractions strictement supérieures à 1 sont celles dont le numérateur est strictement supérieur au dénominateur.
4 > 3 donc 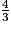 est strictement supérieur à 1.
est strictement supérieur à 1.
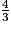 est strictement supérieur à 1.
est strictement supérieur à 1.9 > 2 donc 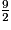 est strictement supérieur à 1.
est strictement supérieur à 1.
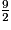 est strictement supérieur à 1.
est strictement supérieur à 1.7 > 2 donc 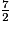 est strictement supérieur à 1.
est strictement supérieur à 1.
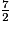 est strictement supérieur à 1.
est strictement supérieur à 1.Il y a donc trois fractions strictement supérieures à 1.
Exercice n°2
On considère les fractions suivantes : 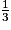 ;
; 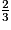 ;
; 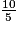 ;
; 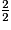 ;
; 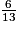 ;
; 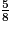 .
.
Dans la liste des fractions ci-dessous, combien y en a-t-il qui sont strictement inférieures à 1 ?
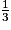 ;
; 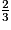 ;
; 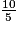 ;
; 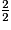 ;
; 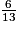 ;
; 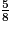 .
.Dans la liste des fractions ci-dessous, combien y en a-t-il qui sont strictement inférieures à 1 ?
Cochez la bonne réponse.
| ||
| ||
| ||
| ||
| ||
| ||
|
Les fractions strictement inférieures à 1 sont celles dont le numérateur est strictement inférieur au dénominateur.
1 < 3 donc 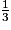 est strictement inférieur à 1.
est strictement inférieur à 1.
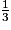 est strictement inférieur à 1.
est strictement inférieur à 1.2 < 3 donc 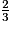 est strictement inférieur à 1.
est strictement inférieur à 1.
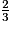 est strictement inférieur à 1.
est strictement inférieur à 1.6 < 13 donc 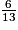 est strictement inférieur à 1.
est strictement inférieur à 1.
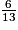 est strictement inférieur à 1.
est strictement inférieur à 1.5 < 8 donc 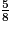 est strictement inférieur à 1.
est strictement inférieur à 1.
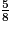 est strictement inférieur à 1.
est strictement inférieur à 1.Il y a donc quatre fractions strictement inférieures à 1.
Exercice n°3
On a rangé les fractions 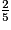 ,
, 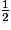 et
et 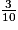 par ordre croissant. Lequel des classements suivants est exact ?
par ordre croissant. Lequel des classements suivants est exact ?
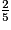 ,
, 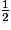 et
et 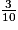 par ordre croissant. Lequel des classements suivants est exact ?
par ordre croissant. Lequel des classements suivants est exact ? Cochez la bonne réponse.
| ||
| ||
|
Toutes les fractions sont inférieures à 1. Pour les comparer, on les écrit avec le même dénominateur 10.
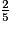 =
= 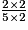 =
= 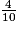
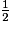 =
= 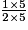 =
= 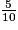
On a : 3 < 4 < 5, donc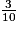 <
< 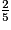 <
< 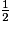 .
.
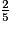 =
= 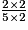 =
= 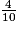
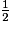 =
= 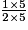 =
= 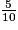
On a : 3 < 4 < 5, donc
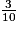 <
< 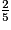 <
< 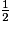 .
.Exercice n°4
On a rangé les fractions 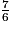 ,
, 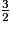 et
et 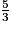 par ordre décroissant. Parmi les classements suivants, lequel est exact ?
par ordre décroissant. Parmi les classements suivants, lequel est exact ?
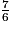 ,
, 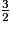 et
et 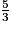 par ordre décroissant. Parmi les classements suivants, lequel est exact ?
par ordre décroissant. Parmi les classements suivants, lequel est exact ? Cochez la bonne réponse.
| ||
| ||
|
Toutes les fractions sont supérieures à 1. Pour les comparer, on les écrit avec le même dénominateur 6.
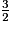 =
= 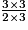 =
= 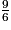
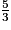 =
= 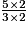 =
= 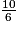
On a : 10 > 9 > 7, donc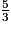 >
> 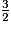 >
> 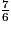 .
.
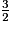 =
= 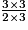 =
= 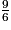
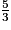 =
= 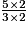 =
= 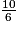
On a : 10 > 9 > 7, donc
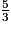 >
> 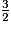 >
> 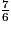 .
.Exercice n°5
On a rangé les fractions 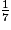 ,
, 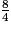 ,
, 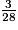 et
et 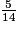 par ordre croissant. Parmi les classements suivants, lequel est exact ?
par ordre croissant. Parmi les classements suivants, lequel est exact ?
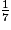 ,
, 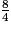 ,
, 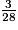 et
et 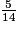 par ordre croissant. Parmi les classements suivants, lequel est exact ?
par ordre croissant. Parmi les classements suivants, lequel est exact ? Cochez la bonne réponse.
| ||
| ||
|
On a 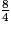 = 2, donc
= 2, donc 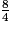 est supérieur à 1. Pour comparer les trois autres fractions, on les écrit au même dénominateur 28.
est supérieur à 1. Pour comparer les trois autres fractions, on les écrit au même dénominateur 28.
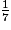 =
= 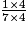 =
= 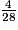
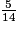 =
= 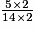 =
= 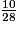
On a : 3 < 4 < 10, donc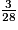 <
< 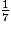 <
< 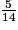 <
< 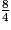 .
.
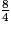 = 2, donc
= 2, donc 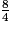 est supérieur à 1. Pour comparer les trois autres fractions, on les écrit au même dénominateur 28.
est supérieur à 1. Pour comparer les trois autres fractions, on les écrit au même dénominateur 28.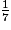 =
= 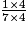 =
= 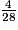
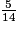 =
= 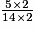 =
= 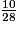
On a : 3 < 4 < 10, donc
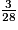 <
< 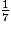 <
< 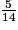 <
< 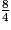 .
.Exercice n°6
On a rangé les fractions 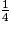 ,
, 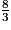 ,
, 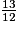 et
et 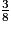 par ordre décroissant. Parmi les classements suivants, lequel est exact ?
par ordre décroissant. Parmi les classements suivants, lequel est exact ?
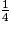 ,
, 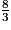 ,
, 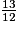 et
et 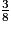 par ordre décroissant. Parmi les classements suivants, lequel est exact ?
par ordre décroissant. Parmi les classements suivants, lequel est exact ? Cochez la bonne réponse.
| ||
| ||
|
Les fractions 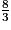 et
et 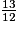 sont supérieures à 1. Pour les comparer, on les écrit au même dénominateur 12.
sont supérieures à 1. Pour les comparer, on les écrit au même dénominateur 12.
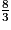 =
= 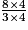 =
= 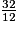
On a : 32 > 13, donc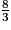 >
> 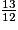 .
.
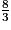 et
et 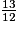 sont supérieures à 1. Pour les comparer, on les écrit au même dénominateur 12.
sont supérieures à 1. Pour les comparer, on les écrit au même dénominateur 12.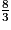 =
= 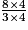 =
= 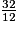
On a : 32 > 13, donc
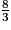 >
> 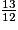 .
.Les fractions 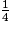 et
et 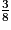 sont inférieures à 1. Pour les comparer, on les écrit au même dénominateur 8.
sont inférieures à 1. Pour les comparer, on les écrit au même dénominateur 8.
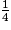 =
= 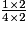 =
= 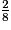
3 > 2, donc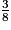 >
> 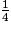 .
.
Donc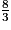 >
> 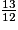 >
> 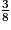 >
> 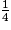 .
.
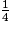 et
et 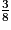 sont inférieures à 1. Pour les comparer, on les écrit au même dénominateur 8.
sont inférieures à 1. Pour les comparer, on les écrit au même dénominateur 8.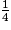 =
= 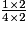 =
= 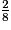
3 > 2, donc
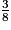 >
> 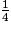 .
.Donc
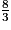 >
> 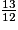 >
> 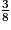 >
> 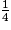 .
.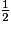 <
< 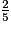 <
< 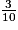
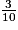 <
< 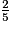 <
< 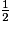
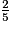 <
< 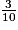 <
< 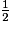
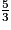 <
< 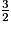 <
< 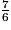
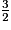 >
> 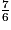 >
> 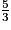
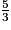 >
> 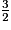 >
> 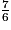
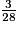 <
< 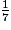 <
< 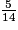 <
< 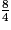
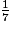 <
< 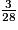 <
< 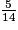 <
< 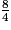
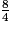 <
< 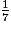 <
< 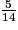 <
< 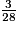
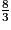 >
> 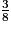 >
> 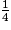 >
> 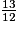
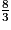 >
> 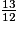 >
> 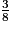 >
> 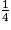
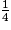 <
< 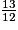 <
< 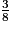 <
<