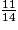Comparons 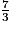 et
et 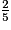 .
.
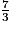 et
et 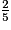 .
.• On remplace chaque fraction par une fraction égale de façon à obtenir deux fractions ayant le même dénominateur.
15 est un multiple de 3 et 5, donc le dénominateur commun des deux fractions est 15.
15 est un multiple de 3 et 5, donc le dénominateur commun des deux fractions est 15.
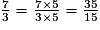
On multiplie le numérateur et le dénominateur de cette fraction par 5.
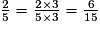
On multiplie le numérateur et le dénominateur de cette fraction par 3.
• On compare les deux numérateurs : 35 > 6 donc 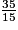 >
> 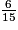 , ou encore
, ou encore 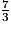 >
> 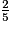 .
.
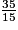 >
> 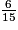 , ou encore
, ou encore 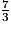 >
> 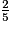 .
.Comparons 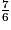 et
et 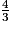 .
.
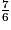 et
et 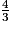 .
.Quand l'un des dénominateurs est multiple de l'autre, on ne remplace qu'une seule des deux fractions.
6 est un multiple de 3, donc le dénominateur commun est 6.
6 est un multiple de 3, donc le dénominateur commun est 6.
• On multiplie le numérateur et le dénominateur de 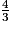 par 2 :
par 2 : 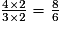 .
.
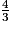 par 2 :
par 2 : 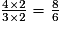 .
.• On compare les numérateurs : 8 > 7, donc 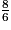 >
> 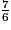 , ou encore
, ou encore 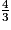 >
> 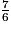 .
.
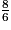 >
> 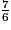 , ou encore
, ou encore 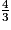 >
> 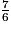 .
.Exercice n°1
Complète avec les nombres qui conviennent.
Écrivez les réponses dans les zones colorées.
Pour comparer 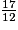 et
et 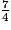 , il faut remplacer
, il faut remplacer 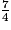 par : /.
par : /.
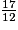 et
et 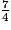 , il faut remplacer
, il faut remplacer 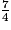 par : /.
par : /.Pour comparer 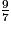 et
et 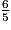 , on réduit les fractions au même dénominateur qui est : .
, on réduit les fractions au même dénominateur qui est : .
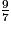 et
et 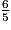 , on réduit les fractions au même dénominateur qui est : .
, on réduit les fractions au même dénominateur qui est : .Deux fractions peuvent être comparées si elles ont le même dénominateur.
12 est un multiple de 4.
On écrit :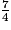 =
= 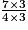 =
= 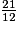 .
.
On écrit :
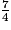 =
= 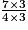 =
= 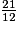 .
.Le plus petit multiple commun à 7 et 5 est 7 × 5.
Exercice n°2
Complète avec le signe < ou >.
Faites glisser les étiquettes dans les zones prévues à cet effet.
>
<
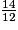
imcAnswer1|imcAnswer4|imcAnswer5?
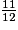
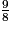
imcAnswer2|imcAnswer3|imcAnswer6?
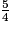
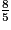
imcAnswer2|imcAnswer3|imcAnswer6?
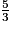
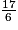
imcAnswer1|imcAnswer4|imcAnswer5?
2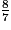
imcAnswer1|imcAnswer4|imcAnswer5?
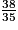
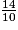
imcAnswer2|imcAnswer3|imcAnswer6?
2,1Le dénominateur commun à 5 et 3 est 5 × 3.
2 = 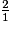 =
= 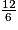
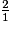 =
= 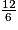
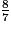 =
= 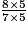 =
= 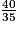
2,1 = 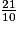
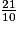
Exercice n°3
Trouve la fraction comprise entre 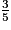 et
et 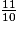 .
.
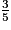 et
et 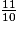 .
. Cochez la bonne réponse.
| ||
| ||
| ||
|
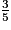 =
= 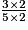 =
= 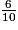 . Il s'agit de trouver la fraction comprise entre
. Il s'agit de trouver la fraction comprise entre 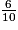 et
et 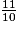 .
.On a :
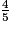 =
= 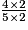 =
= 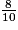 . La fraction cherchée est
. La fraction cherchée est 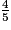 .
.Exercice n°4
Quel est le rangement exact parmi les trois proposés ci-dessous ?
Cochez la bonne réponse.
| ||
| ||
|
Un multiple commun de 3, 5 et 15 est 15. On obtient :
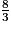 =
= 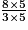 =
= 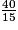
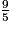 =
= 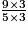 =
= 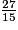
On a : 17 < 27 < 40, donc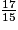 <
< 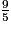 <
< 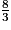 .
.
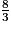 =
= 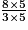 =
= 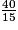
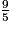 =
= 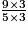 =
= 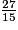
On a : 17 < 27 < 40, donc
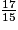 <
< 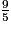 <
< 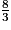 .
.Exercice n°5
Quel est le rangement exact parmi les trois proposés ci-dessous ?
Cochez la bonne réponse.
| ||
| ||
|
Un multiple commun de 6, 7 et 14 est 42. On obtient :
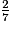 =
= 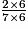 =
= 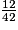
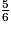 =
= 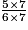 =
= 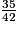
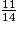 =
= 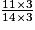 =
= 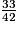
On a : 12 < 33 < 35, donc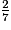 <
< 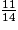 <
< 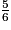 .
.
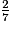 =
= 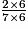 =
= 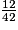
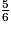 =
= 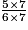 =
= 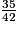
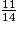 =
= 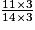 =
= 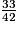
On a : 12 < 33 < 35, donc
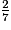 <
< 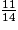 <
< 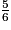 .
.Exercice n°6
L'inégalité 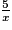 −
− 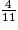 < 0 est-elle vraie pour :
< 0 est-elle vraie pour :
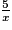 −
− 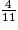 < 0 est-elle vraie pour :
< 0 est-elle vraie pour : Cochez la bonne réponse.
| ||
| ||
| ||
|
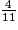 =
= 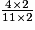 =
= 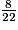 .
.On a : 5 < 8, donc
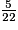 <
< 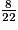 ou encore
ou encore 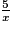 −
− 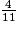 < 0.
< 0.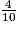
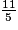
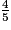
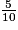
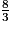 <
< 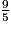 <
< 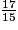
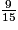 <
< 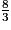 <
< 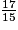
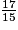 <
< 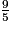 <
< 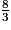
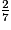 <
< 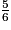 <
< 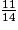
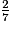 <
< 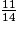 <
< 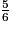
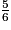 <
<  <
<