Exemple 1
A = 4 + (b − 8)
Les parenthèses sont précédées du signe + ; on peut les supprimer sans transformer l'expression.
A = 4 + b − 8
Exemple 2
B = 4 − (b − 8)
Les parenthèses sont précédées du signe − ; on peut les supprimer à condition de changer les signes qui sont à l'intérieur.
B = 4 − b + 8
Exemple 3
C = 4 − 2(b − 8)
Les parenthèses sont précédées d'une multiplication. On développe.
C = 4 − 2b + 16
Exemple 4
D = a + 2 (3 − (4,5 − a))
• 1re étape : on supprime les parenthèses les plus intérieures.
Elles sont précédées d'un signe −.
Elles sont précédées d'un signe −.
D = a + 2 (3 − 4,5 + a)
D = a + 2 (−1,5 + a)
• 2e étape : on supprime les autres parenthèses en développant le produit.
D = a − 3 + 2a
D = 3a − 3
Exercice n°1
Réduis les expressions ci-dessous.
Attention aux parenthèses.
Attention aux parenthèses.
Écrivez les réponses dans les zones colorées.
1. A = (− x + 2) − (− 5 + x) + 2(5 + x)
A =
A =
2. B = 5x +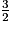 
− 
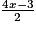
B = x +
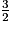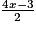
− B = x +
1. A = − x + 2 + 5 − x + 10 + 2x
A = − x − x + 2x + 2 + 5 + 10
A = − 2x + 2x + 17
A = − x − x + 2x + 2 + 5 + 10
A = − 2x + 2x + 17
2. B = 5x +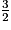 
− 
+ 
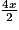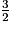
B = 5x +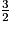
− 2x +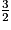 
B = 5x − 2x + 3
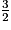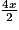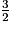
− + B = 5x +
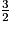− 2x +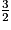 B = 5x − 2x + 3
Exercice n°2
Sur une feuille à part, réduis les expressions, puis coche le bon résultat.
1. A = 3x + (2 − (3 + x)) − 3x
Cochez la bonne réponse.
| ||
|
2. B =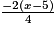 
+ 
− 
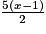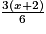
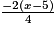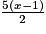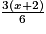
+ − Cochez la bonne réponse.
| ||
|
1.
A = 3x + (2 − 3 − x) − 3x − 15
A = 3x − 1 − x − 3x − 15
A = -x − 1
A = 3x + (2 − 3 − x) − 3x − 15
A = 3x − 1 − x − 3x − 15
A = -x − 1
2.
B =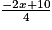
+ 
− 
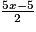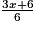
B =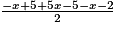
B =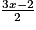
B =
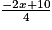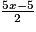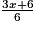
+ − B =
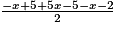
B =
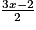
Exercice n°3
Coche la bonne réponse.
a. L'expression 5 − (3x + 2) s'écrit sous forme réduite :
Cochez la bonne réponse.
| ||
| ||
|
b. L'expression (− x + 2) − (−5 + x) + 2 (5 + x) s'écrit sous forme réduite :
Cochez la bonne réponse.
| ||
| ||
|
Attention, pour supprimer des parenthèses précédées d'un signe -, on change les signes des termes qui sont à l'intérieur.
Ainsi : 5 − (3x + 2) = 5 − 3x − 2 = −3x + 3.
Ainsi : 5 − (3x + 2) = 5 − 3x − 2 = −3x + 3.
Exercice n°4
Coche la bonne réponse.
a. L'expression A =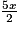 
− (
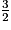− 2x) + 3 s'écrit sous forme réduite :
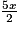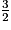− ( − 2x) + 3 s'écrit sous forme réduite : Cochez la bonne réponse.
| ||
| ||
|
+ 
+ 
b. L'expression B = 5 − [4x + (x2 + 5) − (2 − 3x)] s'écrit sous forme réduite :
Cochez la bonne réponse.
| ||
| ||
|
a. A =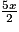 
− (
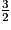− 2x) + 3
A =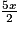
− 
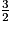+ 2x + 3
A =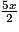
− 
+ 
+ 
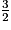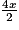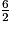
A =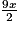
+ 
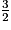
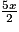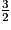− ( − 2x) + 3A =
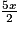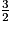− + 2x + 3A =
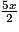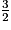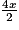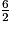
− + + A =
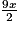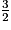
+ b. B = 5 − [4x + (x2 + 5) − (2 − 3x)]
B = 5 − (4x + x2 + 5 − 2 + 3x)
B = 5 − (7x + x2 + 3)
B = 5 − 7x − x2 − 3
B = 2 − 7x − x2
B = 5 − (4x + x2 + 5 − 2 + 3x)
B = 5 − (7x + x2 + 3)
B = 5 − 7x − x2 − 3
B = 2 − 7x − x2
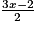
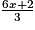
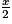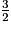
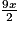