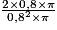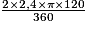Formules
Volume d'une pyramide
Soit une pyramide de hauteur h et dont la base a pour aire B.
Son volume V est donné par la formule : V =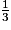 × B × h.
× B × h.
Son volume V est donné par la formule : V =
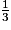 × B × h.
× B × h.Dans cette formule, V, B et h sont exprimés dans des unités correspondantes ; par exemple : h en cm, B en cm2 et V en cm3.
Remarque : une pyramide a pour volume le tiers du volume du prisme droit construit sur sa base et ayant la même hauteur.
Volume d'un cône de révolution
Soit un cône de révolution de hauteur h et dont la base a pour aire B.
Son volume V est donné par la formule : V =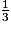 × B × h.
× B × h.
Son volume V est donné par la formule : V =
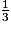 × B × h.
× B × h.Dans cette formule, V, B et h sont exprimés dans des unités correspondantes ; par exemple : h en cm, B en cm2 et V en cm3.
Remarques :
- un cône de révolution a pour volume le tiers du volume du cylindre de révolution construit sur sa base et ayant la même hauteur ;
- si r est le rayon de la base, on a aussi V =
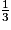 × π × r2 × h.
× π × r2 × h.
Exemple
Calculons le volume d'un cône de révolution dont la base est un disque de rayon 4 cm et dont la hauteur est 7 cm.
On applique la formule :
V =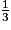 × π × r2 × h.
× π × r2 × h.
V =
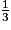 × π × r2 × h.
× π × r2 × h.On a :
V =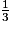 × π × 42 × 7 =
× π × 42 × 7 = 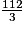 × π
× π 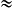 117.
117.
Le volume de ce cône est environ égal à 117 cm3.
V =
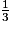 × π × 42 × 7 =
× π × 42 × 7 = 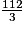 × π
× π 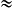 117.
117.Le volume de ce cône est environ égal à 117 cm3.
Exercice n°1
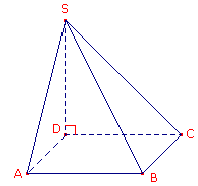 |
SABCD est une pyramide à base carrée dont les dimensions en cm sont : AB = 5 et SD = 6.
Réponds aux questions.
Réponds aux questions.
Écrivez les réponses dans les zones colorées.
1. Quelle est la hauteur de la pyramide SABCD ?
→ cm.
→ cm.
2. Quelle est l'aire de la base de la pyramide SABCD ?
→ cm2.
→ cm2.
3. Quel est le volume de la pyramide SABCD ?
→ cm3.
→ cm3.
• [SD] est la hauteur de la pyramide SABCD.
ABCD est un carré de côté 5 cm, son aire est de 25 cm2.
ABCD est un carré de côté 5 cm, son aire est de 25 cm2.
• Pour calculer le volume on effectue le calcul suivant :
V =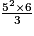 =
= 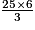 = 25 × 2 = 50.
= 25 × 2 = 50.
V =
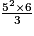 =
= 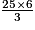 = 25 × 2 = 50.
= 25 × 2 = 50.Exercice n°2
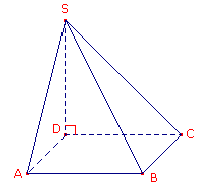 |
Une pyramide SABCD de base carrée a un volume de 48 cm3.
Sa hauteur SD est égale à 4 cm.
Combien mesure le côté de sa base ?
Sa hauteur SD est égale à 4 cm.
Combien mesure le côté de sa base ?
Écrivez la réponse dans la zone colorée.
Réponse : cm.
On calcule d'abord l'aire de la base à l'aide du calcul suivant :
A =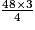 = 12 × 3 = 36.
= 12 × 3 = 36.
A =
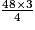 = 12 × 3 = 36.
= 12 × 3 = 36.Exercice n°3
Complète les phrases suivantes.
Écrivez les réponses dans les zones colorées.
1. Une pyramide régulière a une base carrée de côté 10 m ; sa hauteur mesure 9 m.
Son volume est égal à m3.
Son volume est égal à m3.
2. Une autre pyramide régulière de base carrée a une hauteur de 11 m et un volume de 132 m3.
Le côté de sa base mesure m.
Le côté de sa base mesure m.
1. On applique la formule suivante (B est l'aire de la base et h est la hauteur) :
V =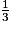 B × h
B × h
V =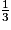 × 100 × 9
× 100 × 9
V =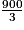 = 300
= 300
Le volume de la pyramide est donc égal à 300 m3.
V =
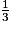 B × h
B × hV =
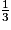 × 100 × 9
× 100 × 9V =
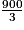 = 300
= 300Le volume de la pyramide est donc égal à 300 m3.
2. On applique à nouveau la formule :
132 =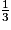 B × 11
B × 11
132 =
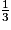 B × 11
B × 11Exercice n°4
vrai ou faux ?
Le volume d'une pyramide est proportionnel à sa hauteur.
Cochez la bonne réponse.
| ||
|
Le volume d'une pyramide est égal au tiers du volume du prisme de même base et de même hauteur.
Cochez la bonne réponse.
| ||
|
Le volume d'un cône est proportionnel au rayon de sa base.
Cochez la bonne réponse.
| ||
|
Le volume d'un cône de rayon 5 cm et de hauteur 9 cm est égal à 236 cm3 (arrondi à l'unité)
Cochez la bonne réponse.
| ||
|
Le coefficient de proportionnalité est égal à 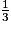 × π × r2.
× π × r2.
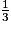 × π × r2.
× π × r2. Rappel : le volume d'un prisme est égal au produit de sa hauteur par l'aire de sa base.
Le coefficient multiplicateur 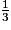 × π × r × h est fonction du rayon r ; il n'y a donc pas proportionnalité.
× π × r × h est fonction du rayon r ; il n'y a donc pas proportionnalité.
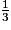 × π × r × h est fonction du rayon r ; il n'y a donc pas proportionnalité.
× π × r × h est fonction du rayon r ; il n'y a donc pas proportionnalité. Exercice n°5
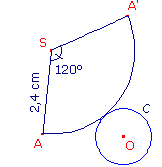 |
La figure ci-contre représente le patron d'un cône de révolution.
Le rayon de la base mesure 0,8 cm.
Le rayon de la base mesure 0,8 cm.
Fais les exercices dans l'ordre proposé.
a. Quel calcul permet de calculer la longueur du cercle C.
Coche la bonne réponse.
Coche la bonne réponse.
Cochez la bonne réponse.
| ||
|
b. Complète avec les valeurs arrondies au centième près.
Écrivez les réponses dans les zones colorées.
Hauteur du cône en cm : .
Volume du cône en cm3 : .
a. La longueur de l'arc entre A et A' est égale à la longueur du cercle C.
b. Pour calculer la hauteur du cône, on utilise le théorème de Pythagore.
h2 = 2,42 − 0,82
h2 = 5,12
h 2,26.
2,26.
h2 = 2,42 − 0,82
h2 = 5,12
h
 2,26.
2,26.