Sujet de métropole, juin 2024, exercice 2

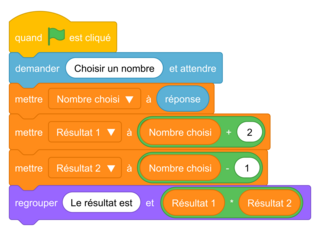
Énoncé

20 points

Programme A

Programme B

$\bullet$ Choisir un nombre.
$\bullet$ Prendre le carré du nombre choisi.
$\bullet$ Multiplier le résultat par 2.
$\bullet$ Ajouter le double du nombre de départ.
$\bullet$ Soustraire 4 au résultat.

Sujet de métropole, juin 2024, exercice 2 - illustration 1

1. a. Vérifier que, si on choisit 5 comme nombre de départ, le résultat du programme A est 56.

b. Quel résultat obtient-on avec le programme B si on choisit – 9 comme nombre de départ ?

Ici, il faut prendre le temps d'effectuer les calculs de chaque programme étape par étape et en notant bien tous vos calculs. Chaque étape de calcul rapporte des points, il faut donc être précis et appliqué dans la rédaction.

2. On choisit un nombre quelconque x comme nombre de départ.

a. Parmi les trois propositions ci-dessous, recopier l'expression qui donne le résultat obtenu par le programme B.

E₁ = (x + 2) − 1

E₂ = (x + 2) × (x − 1)

E₃ = x + 2 × x − 1

Il faut être vigilant sur les priorités impliquées par les calculs entre parenthèses et celles impliquées par l'ordre des calculs dans le programme Scratch.

b. Exprimer en fonction de x le résultat obtenu avec le programme A.

Pour répondre à cette question, il faut reprendre le programme A étape par étape avec le nombre x.
À chaque étape, il faut calculer l'expression littérale et la simplifier le plus possible pour se faciliter la tâche aux étapes de calcul suivantes.

3. Démontrer que, quel que soit le nombre choisi au départ, le résultat du programme A est toujours le double du résultat du programme B.

Il faut penser à comparer les deux expressions littérales. Pour cela, il faut développer l'expression B afin qu'il n'y ait plus de parenthèses et que les deux expressions finales puissent être comparées plus facilement.
Attention à ne pas se contenter d'essayer plusieurs nombres mais bien à utiliser le calcul littéral pour cette question générique.

Voir le corrigé

Corrigé

a. On calcule : 5² = 25 ; 25 × 2 = 50 ; 50 + (5 × 2) = 60 et 60 − 4 = 56. Le résultat obtenu avec le nombre 5 dans le programme A est donc bien 56.

b. On calcule : Résultat 1 = −9 + 2 = −7 ; Résultat 2 = −9 − 1 = − 10 et Résultat final = − 7 × (− 10) = 70. Le résultat obtenu avec le nombre − 9 dans le programme B est donc 70.

2. a. La proposition qui correspond au programme B est E₂ = (x + 2) × (x − 1).

b. On calcule : x² ; x² × 2 = 2x² ; 2x² + (x × 2) = 2x² + 2x et 2x² + 2x − 4. Le résultat obtenu avec x dans le programme A est donc 2x² + 2x − 4.

3. On cherche à trouver si le résultat du programme A est toujours le double du résultat du programme B, soit 2x² + 2x − 4 = 2 × Programme B. Si on développe l'expression du programme B, on obtient :
(x + 2) × (x − 1) = x × x − x × 1 + 2 × x − 2 × 1 = x² − x + 2x − 2 = x² + x − 2.
On observe que le résultat obtenu lors du développement de B est bien la moitié du résultat du programme A. L'affirmation est donc vraie pour tout nombre choisi au départ.