Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2024, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2024, exercice 1
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2024, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2024, exercice 1
Énoncé
20 points
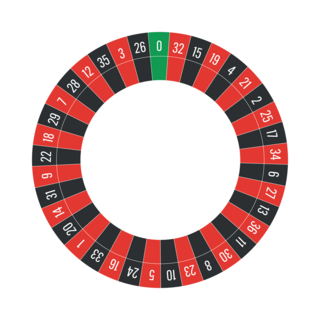
Au casino, la roulette est un jeu de hasard pour lequel chaque joueur mise au choix sur un ou plusieurs numéros. On lance une bille sur une roue qui tourne, numérotée de 0 à 36.
La bille a la même probabilité de s'arrêter sur chaque numéro.
La bille a la même probabilité de s'arrêter sur chaque numéro.
 |
1. Expliquer pourquoi la probabilité que la bille s'arrête sur le numéro 7 est 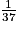 .
.
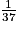 .
.Il faut connaître la définition d'une probabilité. Soyez vigilant et comptez bien toutes les issues possibles pour cette expérience aléatoire.
2. Déterminer la probabilité que la bille s'arrête sur une case à la fois noire et paire.
Faites attention à ne pas oublier d'issues sur la roulette dessinée ci-dessus et pensez bien, ici encore, à tenir compte de toutes les issues concernées.
3. a.
Déterminer la probabilité que la bille s'arrête sur un numéro inférieur ou égal à 6.
b. En déduire la probabilité que la bille s'arrête sur un numéro supérieur ou égal à 7.
Vous ne devez pas recompter les issues possibles pour cette question, mais bien voir qu'elle est reliée à la question précédente car elle concerne toutes les issues qui n'ont pas été utilisées à la question 3. a.
c. Un joueur affirme qu'on a plus de 3 chances sur 4 d'obtenir un numéro supérieur ou égal à 7. A-t-il raison ?
Il faut pouvoir comparer la probabilité obtenue à la question précédente avec ces 3 chances sur 4. Vous pouvez donc utiliser une autre représentation de la probabilité : sous forme de pourcentage ou sous forme décimale, par exemple.
Corrigé
1. Comme il y a 37 numéros sur la roulette (De 0 à 36), il y a bien 1 chance sur 37 d'obtenir chacun d'entre eux, soit 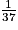 .
.
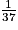 .
.2. Les cases noires et paires sont : 4 ; 2 ; 6 ; 8 ; 10 ; 24 ; 20 ; 22 ; 28 et 26. La probabilité d'obtenir un nombre pair sur une case noire est donc 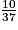 .
.
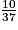 .
.3.
a. Les cases dont les numéros sont inférieurs ou égaux à 6 sont : 0 ; 1 ; 2 ; 3 ; 4 ; 5 et 6. Comme il y a 37 cases, la probabilité d'obtenir un nombre inférieur ou égal à 6 est donc 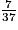 .
.
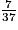 .
.b. Les cases dont les numéros sont supérieurs ou égaux à 7 sont toutes celles qui n'ont pas été citées à la question précédente. La probabilité d'obtenir un nombre supérieur ou égal à 7 est donc 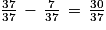 .
.
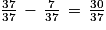 .
.c. On sait que 3 chances sur 4 correspond à 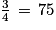 %, alors que la probabilité d'obtenir un nombre supérieur ou égal à 7 est de
%, alors que la probabilité d'obtenir un nombre supérieur ou égal à 7 est de 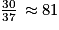 %. Donc le joueur qui fait cette affirmation a bien raison.
%. Donc le joueur qui fait cette affirmation a bien raison.
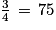 %, alors que la probabilité d'obtenir un nombre supérieur ou égal à 7 est de
%, alors que la probabilité d'obtenir un nombre supérieur ou égal à 7 est de 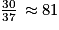 %. Donc le joueur qui fait cette affirmation a bien raison.
%. Donc le joueur qui fait cette affirmation a bien raison.Corrigé
1. Comme il y a 37 numéros sur la roulette (De 0 à 36), il y a bien 1 chance sur 37 d'obtenir chacun d'entre eux, soit 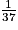 .
.
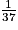 .
.2. Les cases noires et paires sont : 4 ; 2 ; 6 ; 8 ; 10 ; 24 ; 20 ; 22 ; 28 et 26. La probabilité d'obtenir un nombre pair sur une case noire est donc 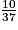 .
.
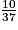 .
.3.
a. Les cases dont les numéros sont inférieurs ou égaux à 6 sont : 0 ; 1 ; 2 ; 3 ; 4 ; 5 et 6. Comme il y a 37 cases, la probabilité d'obtenir un nombre inférieur ou égal à 6 est donc 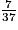 .
.
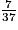 .
.b. Les cases dont les numéros sont supérieurs ou égaux à 7 sont toutes celles qui n'ont pas été citées à la question précédente. La probabilité d'obtenir un nombre supérieur ou égal à 7 est donc 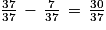 .
.
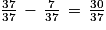 .
.c. On sait que 3 chances sur 4 correspond à 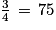 %, alors que la probabilité d'obtenir un nombre supérieur ou égal à 7 est de
%, alors que la probabilité d'obtenir un nombre supérieur ou égal à 7 est de 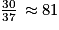 %. Donc le joueur qui fait cette affirmation a bien raison.
%. Donc le joueur qui fait cette affirmation a bien raison.
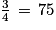 %, alors que la probabilité d'obtenir un nombre supérieur ou égal à 7 est de
%, alors que la probabilité d'obtenir un nombre supérieur ou égal à 7 est de 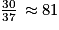 %. Donc le joueur qui fait cette affirmation a bien raison.
%. Donc le joueur qui fait cette affirmation a bien raison.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2024, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2024, exercice 1
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2024, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2024, exercice 1

