Sujet Inde, avril 2014, exercice 6

Énoncé

7 points

Voici le classement des médailles d'or reçues par les participants aux jeux Olympiques pour le cyclisme masculin.

Bilan des médailles d'or de 1896 à 2008

Bilan des médailles d'or de 1896 à 2008
Nation	Or	Nation	Or
France	40	Russie	4
Italie	32	Suisse	3
Royaume-Uni	18	Suède	3
Pays-Bas	15	Tchécoslovaquie	2
États-Unis	14	Norvège	2
Australie	13	Canada	1
Allemagne	13	Afrique du Sud	1
Union soviétique	11	Nouvelle-Zélande	1
Belgique	6	Grèce	1
Danemark	6	Autriche	1
Allemagne de l'Ouest	6	Estonie	1
Espagne	5	Lettonie	1
Allemagne de l'Est	4	Argentine	1

Source : d'après Wikipédia.

Voici un extrait du tableur.

A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
Nombre de médailles d'or	1	2	3	4	5	6	11	14	13	15	18	32	40
Effectif	8	2	2	2	1	3	1	2	1	1	1	1	1	26

Quelle formule a-t-on saisie dans la cellule O2 pour obtenir le nombre total de pays ayant eu une médaille d'or ?

Remarquez que le nombre de la case O2 est une somme.

Calculer la moyenne de cette série (arrondissez à l'unité).

Vous devez trouver une moyenne, arrondie à l'unité, qui est comprise entre 7 et 10.

Déterminer la médiane de cette série.

Rappelez-vous que la médiane d'une série statistique est une valeur qui partage cette série en deux groupes d'effectifs égaux :

un groupe constitué de valeurs inférieures ou égales à la médiane ;
un groupe constitué de valeurs supérieures ou égales à la médiane.

En observant les valeurs prises par la série, donner un argument qui explique pourquoi les valeurs de la moyenne et de la médiane sont différentes.

Remarquez que beaucoup de pays ont un nombre de médailles d'or peu élevé.

Pour le cyclisme masculin, 70 % des pays médaillés ont obtenu au moins une médaille d'or. Quel est le nombre de pays qui n'ont obtenu que des médailles d'argent ou de bronze (arrondir le résultat à l'unité) ?
Si le travail n'est pas terminé, laisser tout de même une trace de la recherche. Elle sera prise en compte dans l'évaluation.

Calculez tout d'abord le nombre total de pays médaillés.
Calculez ensuite le nombre de pays qui n'ont obtenu que des médailles d'argent ou de bronze.

Voir le corrigé

Corrigé

1. Le nombre de la case O2 est la somme des treize nombres de la case B2 à la case N2.
Dans la cellule O2, pour obtenir le nombre total de pays ayant eu une médaille d'or, on a donc écrit la formule « = SOMME(B2:N2) ».

En notant M la moyenne de cette série, on a :
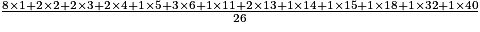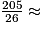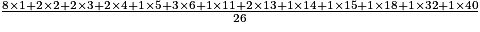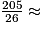M = $\frac{8\times 1 + 2\times 2 +2\times 3 +2\times 4 +1\times 5 +3\times 6 +1\times 11 +2\times 13 + 1\times 14 + 1\times 15+1\times 18 +1\times 32 + 1\times 40}{26}$ = $\frac{205}{26} \approx$ 8 à l'unité près.

La moyenne de cette série est 8, à l'unité près.

b) L'effectif de cette série est 26.
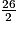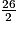$\frac{26}{2}$ = 13, donc la médiane de cette série est la moyenne du treizième et du quatorzième nombre de médailles d'or classés dans l'ordre croissant.
D'après le tableau, le treizième et le quatorzième nombre de médailles d'or classés dans l'ordre croissant est 4.
La médiane du nombre de médailles d'or est donc 4.

c) Le nombre de pays qui ont peu de médailles d'or est elevé : il y a notamment 8 pays qui n'ont gagné qu'une seule médaille d'or.
Il est donc normal que la médiane de cette série soit plus petite que la moyenne.

26 pays correspondent aux 70 % de pays médaillés qui ont obtenu au moins une médaille d'or.
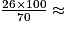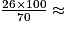À l'aide d'un produit en croix, le nombre total de pays médaillés est donc $\frac{26 \times 100}{70} \approx$ 37 à l'unité près.

Le nombre de pays qui n'ont obtenu que des médailles d'argent ou de bronze est donc 37 − 26 = 11.