Sujet Amérique du Nord, juin 2014, exercice 6

Énoncé

6 points

Pendant le remplissage d'une écluse, Jules et Paul, à bord de leur péniche, patientent en jouant aux dés. Ces dés sont équilibrés.

Jules propose à Paul de jouer avec ces deux dés (un jaune et un rouge).
Il lui explique la règle :

le gagnant est le premier à remporter un total de 1 000 points ;
si, lors d'un lancer, un joueur fait deux « 1 », c'est à dire une paire⁽¹⁾ de « 1 », il remporte 1 000 points (et donc la partie) ;
si un joueur obtient une paire de 3 ou de 4 ou de 5 ou 6, il obtient 100 fois la valeur du dé soit 3 × 100 = 300, ou… ;
si un joueur obtient un résultat autre qu'une paire (par exemple 3 sur le dé jaune et 5 sur le dé rouge), il obtient 50 points.

Est-ce que, lors du jet d'un dé, la probabilité d'obtenir un « 1 » est la même que celle d'obtenir un « 5 » ? Expliquer.

Remarquez que si les dés sont équilibrés, toutes les issues sont équiprobabes.

Jules lance en même temps un dé rouge et un dé jaune. Par exemple, il peut obtenir 3 au dé rouge et 4 au dé jaune, c'est l'une des issues possibles. Expliquer pourquoi le nombre d'issues possibles quand il lance ses deux dés est de 36.

Combien y-a-t-il d'issues possibles pour le dé rouge, et pour le dé jaune ?

Paul a déjà fait 2 lancers et a obtenu 650 points.
Quelle est la probabilité qu'il gagne la partie à son troisième lancer ?

Dans cette question, si le travail n'est pas terminé, laisser tout de même sur la copie une trace de la recherche. Elle sera prise en compte dans la notation.

Combien Paul doit-il obtenir de points au minimum pour gagner la partie à son troisième lancer ?
Cherchez les issues correspondantes, puis calculez la probabilité associée à l'ensemble de ces issues.

(1)On appelle une paire de 1 quand on obtient deux 1, une paire de 2 quand on obtient deux 2…

Voir le corrigé

Corrigé

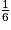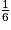1. Les dés sont équilibrés, donc toutes les issues sont équiprobables : P(« obtenir 1 ») = P(« obtenir 5 ») = $\frac{1}{6}$ .

2. Pour le dé rouge, il y a 6 issues possibles et, pour le dé jaune, 6 issues possibles aussi.
Le nombre d'issues possibles quand il lance ses deux dés est donc 6 × 6 = 36.

Pour que Paul gagne la partie à son troisième lancer, il doit obtenir au moins 350 points.
Pour cela, il doit obtenir au troisième lancer :

soit une paire de 1 (1 000 points) ;
soit une paire de 4 (100 × 4 = 400 points) ;
soit une paire de 5 (100 × 5 = 500 points) ;
soit une paire de 6 (100 × 6 = 600 points).

Il y a une issue possible seulement pour chacune des 4 paires qui conviennent. Il y a donc au total 4 issues qui conviennent sur les 36 possibles.

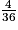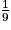La probabilité que Paul gagne la partie à son troisième lancer est $\frac{4}{36}$ = $\frac{1}{9}$ .
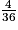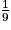