Sujet de métropole, juin 2023, exercice 5

Énoncé

Voici deux programmes de calcul.

Programme A
$\bullet$ Choisir un nombre.
$\bullet$ Multiplier ce nombre par −2.
$\bullet$ Ajouter 5 à ce résultat.

Programme B
$\bullet$ Choisir un nombre.
$\bullet$ Soustraire 5 à ce nombre.
$\bullet$ Multiplier le résultat par 3.
$\bullet$ Ajouter 11 au résultat.

1. a. Montrer que, si on choisit −3 comme nombre de départ, le résultat obtenu avec le programme A est 11.

b. Quel résultat obtient-on avec le programme B si on choisit 5,5 comme nombre de départ ?

Vous devez appliquer les deux programmes de calcul en réalisant les étapes de calcul avec le nombre choisi au départ. Souvenez-vous que vous devez rédiger vos étapes de calcul sur votre copie et pensez à bien noter votre réponse.

2. En désignant par x le nombre de départ, on obtient −2x + 5 comme résultat avec le programme A.
Montrer qu'avec le même nombre de départ, le résultat du programme B est égal à 3x − 4.

Vous devez à présent appliquer le programme de calcul en réalisant les étapes de calcul avec le nombre x. Rédigez bien vos étapes de calcul sur votre copie et pensez à bien détailler vos modifications dans les formules de calcul littéral obtenues.

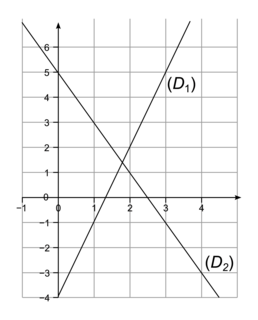
3. a. On a représenté ci-dessous les fonctions f et g définies par f(x) = −2x + 5 et g(x) = 3x − 4.
Associer, en justifiant, chaque droite à la fonction qui lui correspond.

b. Par lecture graphique, donner, le plus précisément possible, le nombre dont l'image est la même par la fonction f et la fonction g.

Dans ces questions, on étudie deux fonctions représentées graphiquement dont on connaît également l'expression. Il faut donc maîtriser le vocabulaire de base des fonctions (image, antécédent, fonction affine, coefficients, etc.) afin de comprendre la représentation graphique proposée et associer correctement les informations aux fonctions étudiées.

4. Déterminer par le calcul le nombre de départ pour lequel les programmes A et B donnent le même résultat.

Cette question est la plus difficile du sujet. Il faut oser entamer une recherche avec les formules obtenues aux questions précédentes, et donc travailler avec des expressions littérales. Ensuite, il ne faut pas hésiter à faire des essais et des tentatives, en rédigeant toutes vos idées sur votre copie pour utiliser au mieux vos connaissances.

Voir le corrigé

Corrigé

1. a. On calcule : −3 × (−2) = 6 puis 6 + 5 = 11.
On obtient donc bien 11 avec le programme A si on choisit −3 comme nombre de départ.

b. On calcule : 5,5 − 5 = 0,5 puis 0,5 × 3 = 1,5 et enfin 1,5 + 11 = 12,5.
On obtient donc 12,5 avec le programme B si on choisit 5,5 comme nombre de départ.

2. On choisit le nombre x au départ du programme B. On calcule alors : x − 5 (qu'on ne peut pas réduire), puis (x − 5) × 3 = 3x − 15 et enfin 3x − 15 + 11 = 3x − 4 (pensez à bien réduire l'expression en regroupant les termes similaires entre eux). On obtient donc bien 3x − 4 avec le programme B si on choisit x au départ.

3. a. La fonction f(x) = −2x + 5 est une fonction affine dont le coefficient directeur a = −2 est négatif, donc quand x augmente de 1, f(x) diminue de 2. Sa représentation graphique est donc la droite D₂.
La fonction g(x) = 3x − 4 est une fonction affine dont le coefficient directeur a = 3 est positif, donc quand x augmente de 1, g(x) augmente de 3. Sa représentation graphique est donc la droite D₁.

Remarque : on peut aussi calculer l'image de 0 ou de 1 pour chaque fonction afin de retrouver les bonnes représentations graphiques.

b. Par lecture graphique, le nombre dont l'image est la même par la fonction f et par la fonction g est environ 1,75 (abscisse du point où les droites se croisent).

4. Pour trouver la valeur de x cherchée, on doit résoudre l'équation f(x) = g(x).
Cela revient à résoudre l'équation : −2x + 5 = 3x − 4.
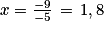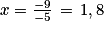On obtient : −2x − 3x = −5 − 4, soit −5x = −9 et donc $x= \frac{-9}{-5}\, = \, 1,8$ .
La valeur pour laquelle les deux programmes donnent le même résultat est donc bien 1,8.