Énoncé
20 points
Une collectionneuse compte ses cartes Pokémon afin de les revendre.
Elle possède 252 cartes de type « feu » et 156 cartes de type « terre ».
Une collectionneuse compte ses cartes Pokémon afin de les revendre.
Elle possède 252 cartes de type « feu » et 156 cartes de type « terre ».
1.
a) Parmi les trois propositions suivantes, laquelle correspond à la décomposition en produit de facteurs premiers du nombre 252 :
| Proposition 1 22 × 9 × 7 | Proposition 2 2 × 2 × 3 × 21 | Proposition 3 22 × 32 × 7 |
b) Donner la décomposition en produit de facteurs premiers du nombre 156.
Prenez le temps de bien réfléchir à la notion de décomposition en produit de facteurs premiers et n'hésitez pas à lister les nombres premiers inférieurs à 30 pour vous aider à réaliser ces deux questions.Pour la question b, notez bien toutes vos étapes de calculs.
2.
Elle veut réaliser des paquets identiques, c'est-à-dire contenant chacun le même nombre de cartes « terre » et le même nombre de cartes « feu » en utilisant toutes ses cartes.
a) Peut-elle faire 36 paquets ?
Ne cherchez pas une résolution trop compliquée pour cette question.
Pensez à bien détailler vos calculs et vos explications.
Pensez à bien détailler vos calculs et vos explications.
b) Quel est le nombre maximum de paquets qu'elle peut réaliser ?
Utilisez les décompositions en produit de facteurs premiers obtenues pour trouver le plus grand diviseur commun aux deux nombres et donc le plus grand nombre de paquets que la collectionneuse peut réaliser. Pensez à bien noter tous vos calculs.
c) Combien de cartes de chaque type contient alors chaque paquet ?
Pensez à bien détailler vos calculs et vos explications.
Pensez à bien terminer la réponse avec une phrase concrète.
Pensez à bien terminer la réponse avec une phrase concrète.
3. Elle choisit une carte au hasard parmi toutes ses cartes. On suppose les cartes indiscernables au toucher. Calculer la probabilité que ce soit une carte de type « terre ».
Vous devez ici utiliser vos connaissances sur les probabilités pour résoudre cette question. Votre réponse peut être écrite sous différentes formes (fraction, nombre décimal ou pourcentage), mais vous devez dans tous les cas écrire vos étapes de calcul.
Corrigé
1.
a) Comme les nombres 9 et 21 ne sont pas des nombres premiers, cela élimine les propositions 1 et 2 qui ne sont donc pas les décompositions cherchées.
La décomposition en produit de facteurs premiers de 252 est donc obtenue avec la proposition 3 : 2² × 32 × 7.
La décomposition en produit de facteurs premiers de 252 est donc obtenue avec la proposition 3 : 2² × 32 × 7.
b) On calcule la décomposition : 126 = 2 × 78 = 2 × 2 × 39 = 22 × 3 × 13.
La décomposition en produit de facteurs premiers du nombre 156 est donc 22 × 3 × 13.
La décomposition en produit de facteurs premiers du nombre 156 est donc 22 × 3 × 13.
2.
a) Le nombre 156 n'est pas divisible par 36 car 156 ÷ 36  4,33.
4,33.
Elle ne peut donc pas réaliser 36 paquets avec ses cartes.
 4,33.
4,33.Elle ne peut donc pas réaliser 36 paquets avec ses cartes.
b) La décomposition en produit de facteurs premiers du nombre 252 est : 22 × 32 × 7 et celle du nombre 156 est : 22 × 3 × 13.
Ces deux nombres ont donc 22 × 3 en commun dans leurs décompositions en produit de facteurs premiers. Comme 22 × 3 = 12, le plus grand diviseur commun aux nombres 252 et 156 est donc 12.
La collectionneuse peut donc réaliser 12 paquets au maximum.
Ces deux nombres ont donc 22 × 3 en commun dans leurs décompositions en produit de facteurs premiers. Comme 22 × 3 = 12, le plus grand diviseur commun aux nombres 252 et 156 est donc 12.
La collectionneuse peut donc réaliser 12 paquets au maximum.
c) On calcule le nombre de cartes par paquet : 252 ÷ 12 = 21 et 156 ÷ 12 = 13.
Dans chaque paquet, il y aura donc 21 cartes Pokémon de type « feu » et 13 cartes Pokémon de type « terre ».
Dans chaque paquet, il y aura donc 21 cartes Pokémon de type « feu » et 13 cartes Pokémon de type « terre ».
3. Au total, cette collectionneuse possède 408 cartes Pokémon (252 + 156 = 408).
La probabilité qu'elle tire une carte de type « terre » dans son paquet est donc égale à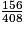 qui se simplifie par 12 et donne
qui se simplifie par 12 et donne 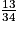 ou encore environ 0,38 en nombre décimal soit 38 %.
ou encore environ 0,38 en nombre décimal soit 38 %.
La probabilité qu'elle tire une carte de type « terre » dans son paquet est donc égale à
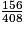 qui se simplifie par 12 et donne
qui se simplifie par 12 et donne 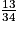 ou encore environ 0,38 en nombre décimal soit 38 %.
ou encore environ 0,38 en nombre décimal soit 38 %.
