Énoncé
20 points
Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n'est demandée. Pour chaque question, trois réponses (A, B et C) sont proposées. Une seule réponse est exacte. Recopier sur la copie le numéro de la question et la réponse.
Partie A
Une urne contient 7 jetons verts, 4 jetons rouges, 3 jetons bleus et 2 jetons jaunes. Les jetons sont indiscernables au toucher. On pioche un jeton au hasard dans cette urne.
| Questions | Réponse A | Réponse B | Réponse C |
|---|---|---|---|
1. À quel événement correspond une probabilité de 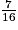 ? | Obtenir un jeton de couleur rouge ou jaune. | Obtenir un jeton qui n'est pas vert. | Obtenir un jeton vert. |
| 2. Quelle est la probabilité de ne pas tirer un jeton bleu ? |  |  |  |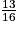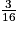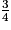
Il faut que vous pensiez à calculer le nombre total d'issues de cette expérience pour bien analyser la situation et ne pas choisir la réponse trop précipitamment.
Les questions de ce QCM sont ici assez simples, et rapportent chacune 4 points, il faut donc bien prendre son temps pour y répondre correctement.
Les questions de ce QCM sont ici assez simples, et rapportent chacune 4 points, il faut donc bien prendre son temps pour y répondre correctement.
Partie B
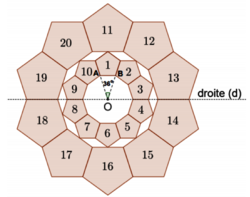
On considère la figure suivante, composée de vingt motifs numérotés de 1 à 20, dans laquelle :
• 
.
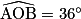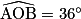.• Le motif 11 est l'image du motif 1 par l'homothétie de centre O et de rapport 2.
 |
| Questions | Réponse A | Réponse B | Réponse C |
|---|---|---|---|
| 3. Quelle est l'image du motif 20 par la symétrie d'axe de la droite (d) ? | Le motif 17 | Le motif 15 | Le motif 12 |
| 4. Par quelle rotation le motif 3 est-il l'image du motif 1 ? | Une rotation de centre O, et d'angle 36°. | Une rotation de centre O, et d'angle 72° | Une rotation de centre O, et d'angle 90°. |
| 5. L'aire du motif 11 est égale : | au double de l'aire du motif 1. | à 4 fois l'aire du motif 1. | À la moitié de l'aire du motif 1. |
Mettez les éléments significatifs de chaque transformation en couleur pour mieux visualiser les figures initiales et les figures obtenues et ainsi mieux répondre.
Pour la rotation, vous devez compter le nombre de « cran » de décalage de la figure initiale lors de la rotation pour obtenir l'angle par un calcul en fonction de ces crans.
Pour l'homothétie, vous devez vous souvenir que le rapport d'agrandissement s'applique aux longueurs. Les aires sont alors multipliées par le même coefficient, mais au carré.
Pour la rotation, vous devez compter le nombre de « cran » de décalage de la figure initiale lors de la rotation pour obtenir l'angle par un calcul en fonction de ces crans.
Pour l'homothétie, vous devez vous souvenir que le rapport d'agrandissement s'applique aux longueurs. Les aires sont alors multipliées par le même coefficient, mais au carré.
Corrigé
Partie A
1. Au total, il y a 16 jetons car : 7 + 4 + 3 + 2 = 16.
Donc la probabilité de piocher un jeton vert est de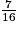
Réponse C.
Donc la probabilité de piocher un jeton vert est de
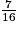Réponse C. 2. Si le jeton n'est pas bleu, il peut être vert, rouge ou jaune. On a donc une probabilité de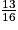 
de ne pas piocher un jeton bleu. Réponse A.
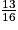de ne pas piocher un jeton bleu. Réponse A.Partie B
1. L'image du pentagone 20 par la symétrie axiale d'axe (d) est le pentagone 17. Réponse A.
2. Le pentagone 3 est l'image du pentagone 1 par la rotation de centre O et d'angle 72°, car on calcule 36° × 2. Réponse B.
3. Le pentagone 11 est l'image du pentagone 1 par l'homothétie de centre O et de rapport 2. C'est donc un agrandissement de rapport 2, donc l'aire de la figure est multipliée par 22 soit 4. Réponse B.
