Énoncé
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant soigneusement la réponse.
1.
Un sac contient 6 jetons rouges, 2 jetons jaunes et des jetons verts.
La probabilité de tirer un jeton vert vaut 0,5.
Affirmation : le sac contient 4 jetons verts.
La probabilité de tirer un jeton vert vaut 0,5.
Affirmation : le sac contient 4 jetons verts.
Remarquez que si la probabilité de tirer un jeton vert est 0,5, alors le nombre de jetons verts est égal à la moitié de l'ensemble des jetons.
2.
En informatique, on utilise comme unités de mesure les multiples suivants de l'octet :
1 Ko = 103 octets, 1 Mo = 106 octets, 1 Go = 109 octets, 1 To = 1012 octets,
où Ko est l'abréviation de kilooctet, Mo celle de mégaoctet, Go celle de gigaoctet, To celle de téraoctet.
On partage un disque dur de 1,5 To en dossiers de 60 Go chacun.
Affirmation : on obtient ainsi 25 dossiers.
1 Ko = 103 octets, 1 Mo = 106 octets, 1 Go = 109 octets, 1 To = 1012 octets,
où Ko est l'abréviation de kilooctet, Mo celle de mégaoctet, Go celle de gigaoctet, To celle de téraoctet.
On partage un disque dur de 1,5 To en dossiers de 60 Go chacun.
Affirmation : on obtient ainsi 25 dossiers.
Convertissez 1,5 To en gigaoctets.
3.
Sur la figure codée ci-après, les points B, A et E sont alignés.
Affirmation : l'angle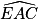 mesure
mesure 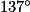 .
.
Affirmation : l'angle
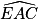 mesure
mesure 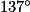 .
.Notez x la mesure de l'angle 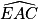 et exprimez ensuite la mesure de l'angle
et exprimez ensuite la mesure de l'angle 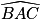 de deux façons.
de deux façons.
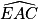 et exprimez ensuite la mesure de l'angle
et exprimez ensuite la mesure de l'angle 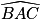 de deux façons.
de deux façons.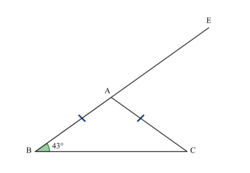 |
4.
Un verre de forme conique est complètement rempli.
On verse son contenu de sorte que la hauteur du liquide soit divisée par 2.
Affirmation : le volume du liquide est divisé par 6.
On verse son contenu de sorte que la hauteur du liquide soit divisée par 2.
Affirmation : le volume du liquide est divisé par 6.
Remarquez que le cône que forme le liquide lorsque sa hauteur a été divisée par 2 est une réduction du cône que forme l'intérieur du verre rempli.
 |
Corrigé
1.
L'affirmation est fausse.
Si le sac contenait 4 jetons verts, alors le sac contiendrait au total :
6 + 2 + 4 = 12 jetons.
La probabilité de tirer un jeton vert serait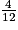 =
= 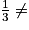 0,5, donc l'affirmation est fausse.
0,5, donc l'affirmation est fausse.
6 + 2 + 4 = 12 jetons.
La probabilité de tirer un jeton vert serait
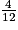 =
= 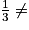 0,5, donc l'affirmation est fausse.
0,5, donc l'affirmation est fausse.Cherchons le nombre de jetons verts nécessaires, noté x, pour que la probabilité de tirer un jeton vert soit 0,5.
Si la probabilité de tirer un jeton vert est 0,5, on a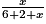 = 0,5, puis :
= 0,5, puis :
x = 0,5 × (8 + x) = 0,5 × 8 + 0,5 × x = 4 + 0,5x et x − 0,5x = 0,5x = 4.
On a donc x = 2 × 4 = 8.
Pour que la probabilité de tirer un jeton vert dans ce sac soit 0,5, le sac doit contenir 8 jetons verts : autant de jetons verts que de jetons rouges et jaunes.
Si la probabilité de tirer un jeton vert est 0,5, on a
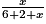 = 0,5, puis :
= 0,5, puis :x = 0,5 × (8 + x) = 0,5 × 8 + 0,5 × x = 4 + 0,5x et x − 0,5x = 0,5x = 4.
On a donc x = 2 × 4 = 8.
Pour que la probabilité de tirer un jeton vert dans ce sac soit 0,5, le sac doit contenir 8 jetons verts : autant de jetons verts que de jetons rouges et jaunes.
2.
L'affirmation est vraie.
On a 1,5 To = 1,5 × 103 Go = 1 500 Go.
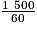 = 25 donc si on partage un disque dur de 1,5 To en dossiers de 60 Go chacun, on obtient 25 dossiers.
= 25 donc si on partage un disque dur de 1,5 To en dossiers de 60 Go chacun, on obtient 25 dossiers.
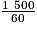 = 25 donc si on partage un disque dur de 1,5 To en dossiers de 60 Go chacun, on obtient 25 dossiers.
= 25 donc si on partage un disque dur de 1,5 To en dossiers de 60 Go chacun, on obtient 25 dossiers.3.
L'affirmation est fausse.
Notons x la mesure de l'angle 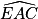 et exprimons la mesure de l'angle
et exprimons la mesure de l'angle 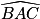 de deux façons.
de deux façons.
Les points B, A et E étant alignés, on a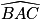 =
= 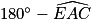 =
= 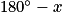 .
.
Aussi, la somme des angles d'un triangle étant de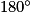 , on a :
, on a :
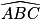 +
+ 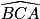 +
+ 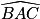 =
= 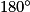 ;
;
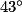 +
+ 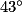 +
+ 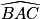 =
= 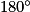 , car le triangle BAC est isocèle en A,
, car le triangle BAC est isocèle en A,
donc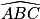 =
= 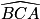 =
= 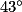 .
.
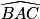 =
= 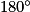 − 2 ×
− 2 × 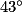 .
.
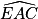 et exprimons la mesure de l'angle
et exprimons la mesure de l'angle 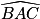 de deux façons.
de deux façons.Les points B, A et E étant alignés, on a
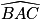 =
= 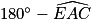 =
= 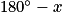 .
.Aussi, la somme des angles d'un triangle étant de
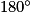 , on a :
, on a :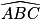 +
+ 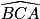 +
+ 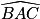 =
= 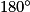 ;
;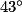 +
+ 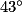 +
+ 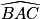 =
= 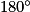 , car le triangle BAC est isocèle en A,
, car le triangle BAC est isocèle en A,donc
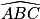 =
= 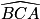 =
= 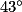 .
.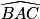 =
= 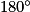 − 2 ×
− 2 × 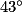 .
.D'après les deux expressions de la mesure de l'angle 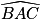 , on a :
, on a :
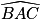 =
= 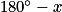 =
= 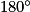 − 2 ×
− 2 × 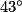 , donc x = 2 ×
, donc x = 2 × 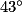 =
= 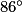 .
.
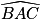 , on a :
, on a :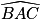 =
= 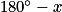 =
= 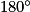 − 2 ×
− 2 × 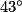 , donc x = 2 ×
, donc x = 2 × 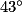 =
= 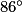 .
.4.
L'affirmation est fausse.
Le nouveau cône que forme le liquide lorsque sa hauteur a été divisée par 2 est une réduction de rapport 2 du cône que forme l'intérieur du verre rempli.
Or, une réduction de rapport k multiplie les volumes par k3, donc ici par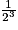 =
= 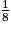 car k =
car k = 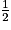 .
.
Lorsque la hauteur du liquide est divisée par 2, le volume du liquide est divisé par 8.
Or, une réduction de rapport k multiplie les volumes par k3, donc ici par
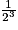 =
= 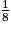 car k =
car k = 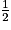 .
.Lorsque la hauteur du liquide est divisée par 2, le volume du liquide est divisé par 8.

