Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 9
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 9
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 9
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 9
Énoncé
5 points
Certaines écluses ont des portes dites « busquées », qui forment un angle pointé vers l'amont de manière à résister à la pression de l'eau.
En vous appuyant sur le schéma ci-dessous, déterminer la longueur des portes au cm près.
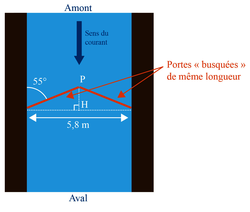 |
Si le travail n'est pas terminé, laisser tout de même une trace de la recherche. Elle sera prise en compte dans la notation.
Pensez à utiliser les propriétés du triangle isocèle, puis une relation trigonométrique pour calculer la longueur AP d'une porte busquée.
Corrigé
PA = PB donc le triangle APB est isocèle en P.
Dans un triangle isocèle, la hauteur issue du sommet principal est aussi médiatrice : on a donc AH =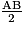 =
= 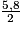 = 2,9 m.
= 2,9 m.
Dans un triangle isocèle, la hauteur issue du sommet principal est aussi médiatrice : on a donc AH =
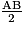 =
= 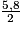 = 2,9 m.
= 2,9 m.On a 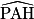 =
= 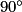 −
− 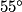 =
= 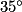 .
.
Dans le triangle PAH rectangle en H, on a :
cos(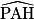 ) =
) = 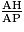 donc :
donc :
AP =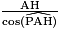 puis :
puis :
AP =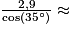 3,54 m au centimètre près.
3,54 m au centimètre près.
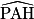 =
= 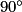 −
− 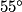 =
= 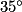 .
.Dans le triangle PAH rectangle en H, on a :
cos(
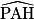 ) =
) = 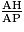 donc :
donc :AP =
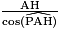 puis :
puis :AP =
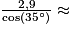 3,54 m au centimètre près.
3,54 m au centimètre près.La longueur de chacune des deux portes dites « busquées » est de 3,54 m environ.
Corrigé
PA = PB donc le triangle APB est isocèle en P.
Dans un triangle isocèle, la hauteur issue du sommet principal est aussi médiatrice : on a donc AH =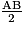 =
= 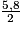 = 2,9 m.
= 2,9 m.
Dans un triangle isocèle, la hauteur issue du sommet principal est aussi médiatrice : on a donc AH =
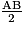 =
= 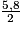 = 2,9 m.
= 2,9 m.On a 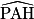 =
= 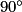 −
− 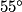 =
= 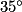 .
.
Dans le triangle PAH rectangle en H, on a :
cos(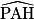 ) =
) = 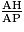 donc :
donc :
AP =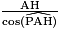 puis :
puis :
AP =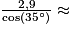 3,54 m au centimètre près.
3,54 m au centimètre près.
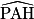 =
= 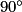 −
− 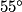 =
= 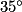 .
.Dans le triangle PAH rectangle en H, on a :
cos(
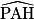 ) =
) = 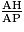 donc :
donc :AP =
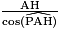 puis :
puis :AP =
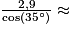 3,54 m au centimètre près.
3,54 m au centimètre près.La longueur de chacune des deux portes dites « busquées » est de 3,54 m environ.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 9
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 9
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 9
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 9

