Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 4
Énoncé
5 points
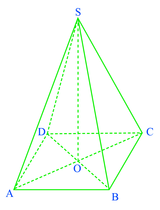 |
Paul en visite à Paris admire la Pyramide, réalisée en verre feuilleté au centre de la cour intérieure du Louvre.
Cette pyramide régulière a :
Cette pyramide régulière a :
- pour base un carré ABCD de côté 35 mètres ;
- pour hauteur le segment [SO] de longueur 22 mètres.
Paul a tellement apprécié cette pyramide qu'il achète comme souvenir de sa visite une lampe à huile dont le réservoir en verre est une réduction à l'échelle 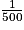 de la vraie pyramide.
de la vraie pyramide.
Le mode d'emploi de la lampe précise que, une fois allumée, elle brûle 4 cm3 d'huile par heure.
Au bout de combien de temps ne restera-t-il plus d'huile dans le réservoir ? Arrondir à l'unité d'heures.
Rappel : Volume d'une pyramide = un tiers du produit de l'aire de la base par la hauteur.
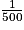 de la vraie pyramide.
de la vraie pyramide. Le mode d'emploi de la lampe précise que, une fois allumée, elle brûle 4 cm3 d'huile par heure.
Au bout de combien de temps ne restera-t-il plus d'huile dans le réservoir ? Arrondir à l'unité d'heures.
Rappel : Volume d'une pyramide = un tiers du produit de l'aire de la base par la hauteur.
Faire apparaître sur la copie la démarche utilisée. Toute trace de recherche sera prise en compte lors de l'évaluation même si le travail n'est pas complètement abouti.
Commencez par calculer le volume de la pyramide SABCD en m3, puis calculez le volume de sa réduction à l'échelle 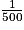 en cm3.
en cm3.
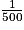 en cm3.
en cm3.Corrigé
Le volume de la pyramide à base carrée SABCD est :
V =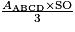 =
= 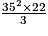 =
= 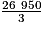 m3.
m3.
V =
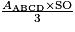 =
= 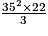 =
= 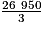 m3.
m3. Une réduction de rapport 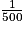 multiplie les volumes par
multiplie les volumes par 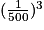 =
= 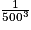 =
= 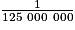 .
.
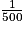 multiplie les volumes par
multiplie les volumes par 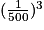 =
= 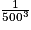 =
= 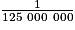 .
.Le volume de la lampe à huile qui est une réduction à l'échelle 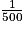 de la vraie pyramide est donc :
de la vraie pyramide est donc :
V' =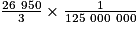 m3
m3
V' =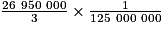 dm3
dm3
V' =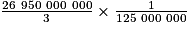 cm3
cm3
V' =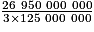 cm3
cm3
V' =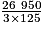 cm3
cm3
V' =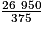 cm3
cm3
V' 71,9 cm3 au dixième près.
71,9 cm3 au dixième près.
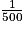 de la vraie pyramide est donc :
de la vraie pyramide est donc :V' =
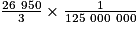 m3
m3 V' =
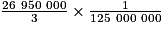 dm3
dm3 V' =
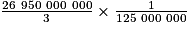 cm3
cm3 V' =
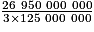 cm3
cm3 V' =
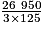 cm3
cm3 V' =
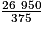 cm3
cm3V'
 71,9 cm3 au dixième près.
71,9 cm3 au dixième près. La lampe à huile brûle 4 cm3 d'huile par heure donc il ne restera plus d'huile au bout d'environ 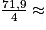 18 h arrondi à l'unité d'heures près.
18 h arrondi à l'unité d'heures près.
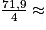 18 h arrondi à l'unité d'heures près.
18 h arrondi à l'unité d'heures près. Corrigé
Le volume de la pyramide à base carrée SABCD est :
V =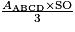 =
= 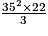 =
= 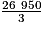 m3.
m3.
V =
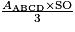 =
= 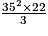 =
= 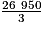 m3.
m3. Une réduction de rapport 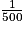 multiplie les volumes par
multiplie les volumes par 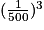 =
= 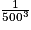 =
= 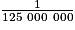 .
.
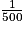 multiplie les volumes par
multiplie les volumes par 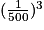 =
= 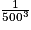 =
= 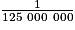 .
.Le volume de la lampe à huile qui est une réduction à l'échelle 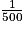 de la vraie pyramide est donc :
de la vraie pyramide est donc :
V' =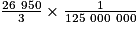 m3
m3
V' =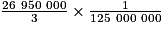 dm3
dm3
V' =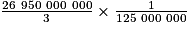 cm3
cm3
V' =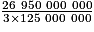 cm3
cm3
V' =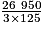 cm3
cm3
V' =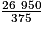 cm3
cm3
V' 71,9 cm3 au dixième près.
71,9 cm3 au dixième près.
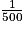 de la vraie pyramide est donc :
de la vraie pyramide est donc :V' =
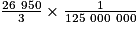 m3
m3 V' =
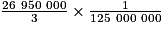 dm3
dm3 V' =
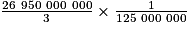 cm3
cm3 V' =
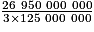 cm3
cm3 V' =
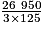 cm3
cm3 V' =
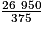 cm3
cm3V'
 71,9 cm3 au dixième près.
71,9 cm3 au dixième près. La lampe à huile brûle 4 cm3 d'huile par heure donc il ne restera plus d'huile au bout d'environ 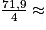 18 h arrondi à l'unité d'heures près.
18 h arrondi à l'unité d'heures près.
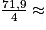 18 h arrondi à l'unité d'heures près.
18 h arrondi à l'unité d'heures près.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 4

