Nouveau message
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Énoncé
4 points
L'exercice suivant traite du thème « le canal du Midi »(1). Le vocabulaire spécifique est donné sur le schéma ci-dessous.
 |
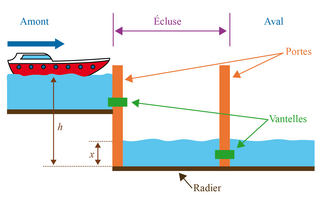Le débit moyen q d'un fluide dépend de la vitesse moyenne v du fluide et de l'aire de la section d'écoulement d'aire S. Il est donné par la formule suivante :
q = S × v où q est exprimé en m3.s−1 ; S est exprimé en m2 ; v est exprimé en m.s−1.
Pour cette partie, on considérera que la vitesse moyenne d'écoulement de l'eau à travers la vantelle durant le remplissage est v = 2,8 m.s−1.
La vantelle a la forme d'un disque de rayon R = 30 cm.
q = S × v où q est exprimé en m3.s−1 ; S est exprimé en m2 ; v est exprimé en m.s−1.
Pour cette partie, on considérera que la vitesse moyenne d'écoulement de l'eau à travers la vantelle durant le remplissage est v = 2,8 m.s−1.
La vantelle a la forme d'un disque de rayon R = 30 cm.
1.
Quelle est l'aire exacte, en m2, de la vantelle ?
L'aire d'un disque de rayon R est πR2. Faites attention aux unités dans le calcul.
2.
Déterminer le débit moyen arrondi au millième de cette vantelle durant le remplissage.
Pour calculer q, remplacez S et v par les valeurs données dans l'énoncé.
3.
Pendant combien de secondes faudra-t-il patienter pour le remplissage d'une écluse de capacité 756 m3 ? Est-ce que l'on attendra plus de 15 minutes ?
Rappelez-vous que la formule du débit est donnée par D =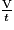 
(m3.s−1) où V est le volume (m3), t est le temps (s).
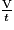(m3.s−1) où V est le volume (m3), t est le temps (s).(1)Le canal du Midi est un canal qui rejoint l'Atlantique à la Méditerranée.
Corrigé
1.
L'aire d'un disque de rayon R est πR2.
La vantelle a la forme d'un disque de rayon R = 30 cm = 0,3 m donc son aire exacte est S = π × 0,32 = 0,09π m2.
La vantelle a la forme d'un disque de rayon R = 30 cm = 0,3 m donc son aire exacte est S = π × 0,32 = 0,09π m2.
2.
Le débit moyen arrondi au millième de cette vantelle durant le remplissage est donné par la formule q = S × v avec S = 0,09π m2 et v = 2,8 m.s−1.
On a donc : q = 0,09π × 2,8 = 0,252π
0,792 m3.s−1 au millième près en utilisant la touche « π » de la calculatrice.
On a donc : q = 0,09π × 2,8 = 0,252π
0,792 m3.s−1 au millième près en utilisant la touche « π » de la calculatrice. 3.
En notant t (en secondes) le temps qu'il faudra pour remplir une écluse de 756 m3, on a :
0,792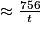
donc t 
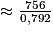= 955 s à l'unité près.
0,792
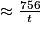donc t 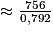= 955 s à l'unité près. 955 s = 15 × 60 + 55 s = 15 min 55 s.
Le temps de remplissage d'une écluse de capacité 756 m3 est 15 min 55 s, donc il faudra attendre plus de 15 minutes.
Le temps de remplissage d'une écluse de capacité 756 m3 est 15 min 55 s, donc il faudra attendre plus de 15 minutes.
Corrigé
1.
L'aire d'un disque de rayon R est πR2.
La vantelle a la forme d'un disque de rayon R = 30 cm = 0,3 m donc son aire exacte est S = π × 0,32 = 0,09π m2.
La vantelle a la forme d'un disque de rayon R = 30 cm = 0,3 m donc son aire exacte est S = π × 0,32 = 0,09π m2.
2.
Le débit moyen arrondi au millième de cette vantelle durant le remplissage est donné par la formule q = S × v avec S = 0,09π m2 et v = 2,8 m.s−1.
On a donc : q = 0,09π × 2,8 = 0,252π 0,792 m3.s−1 au millième près en utilisant la touche « π » de la calculatrice.
On a donc : q = 0,09π × 2,8 = 0,252π
0,792 m3.s−1 au millième près en utilisant la touche « π » de la calculatrice. 3.
En notant t (en secondes) le temps qu'il faudra pour remplir une écluse de 756 m3, on a :
0,792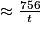 donc t 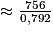= 955 s à l'unité près.
0,792
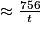donc t 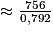= 955 s à l'unité près. 955 s = 15 × 60 + 55 s = 15 min 55 s.
Le temps de remplissage d'une écluse de capacité 756 m3 est 15 min 55 s, donc il faudra attendre plus de 15 minutes.
Le temps de remplissage d'une écluse de capacité 756 m3 est 15 min 55 s, donc il faudra attendre plus de 15 minutes.
Nouveau message
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 8
