Nouveau message
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Énoncé
3 points
À Pise vers 1200 après J.-C. (problème attribué à Léonard de Pise, dit Fibonacci, mathématicien italien du Moyen Âge).
Une lance, longue de 20 pieds(1), est posée verticalement le long d'une tour considérée comme perpendiculaire au sol. Si on éloigne l'extrémité de la lance qui repose sur le sol de 12 pieds de la tour, de combien descend l'autre extrémité de la lance le long du mur ?
 |
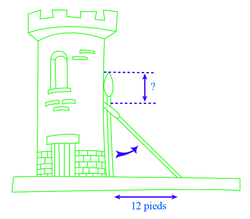Il s'agit de mettre en équation (d'inconnue h) le problème en utilisant le théorème de Pythagore.
Il faudra écrire l'équation sous la forme d'une différence de deux carrés égale à 0 et utiliser une identité remarquable.
Il faudra écrire l'équation sous la forme d'une différence de deux carrés égale à 0 et utiliser une identité remarquable.
(1)Un pied est une unité de mesure anglo-saxonne valant environ 30 cm.
Corrigé
Voici une représentation géométrique de la tour :
 |
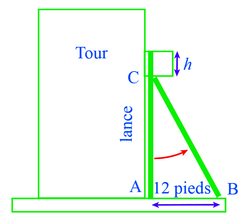Dans le triangle ABC rectangle en A, on a : AC = 20 − h ; AB = 12 ; BC = 20.
D'après le théorème de Pythagore, on a :
BC2 = AB2 + AC2
202 = 122 + (20 − h)2 en remplaçant les distances par leur expression ou valeurs.
(20 − h)2 = 400 − 144 = 256 = 162
(20 − h)2 − 162 = 0
(20 − h − 16)(20 − h + 16) = 0 en utilisant l'identité remarquable a2 − b2 = (a − b)(a + b).
(4 − h)(36 − h) = 0 qui est une équation produit.
4 − h = 0 ou 36 − h = 0 car un produit est nul si et seulement si l'un de ses facteurs est nul.
h = 4 ou h = 36.
BC2 = AB2 + AC2
202 = 122 + (20 − h)2 en remplaçant les distances par leur expression ou valeurs.
(20 − h)2 = 400 − 144 = 256 = 162
(20 − h)2 − 162 = 0
(20 − h − 16)(20 − h + 16) = 0 en utilisant l'identité remarquable a2 − b2 = (a − b)(a + b).
(4 − h)(36 − h) = 0 qui est une équation produit.
4 − h = 0 ou 36 − h = 0 car un produit est nul si et seulement si l'un de ses facteurs est nul.
h = 4 ou h = 36.
La distance h est inférieure à 20, donc la seule solution qui convient est h = 4 pieds.
La longueur d'un pied est proche de 30 cm donc h
4 × 30 = 120 cm.
La longueur d'un pied est proche de 30 cm donc h
4 × 30 = 120 cm. Corrigé
Voici une représentation géométrique de la tour :
|
Dans le triangle ABC rectangle en A, on a : AC = 20 − h ; AB = 12 ; BC = 20.
D'après le théorème de Pythagore, on a :
BC2 = AB2 + AC2
202 = 122 + (20 − h)2 en remplaçant les distances par leur expression ou valeurs.
(20 − h)2 = 400 − 144 = 256 = 162
(20 − h)2 − 162 = 0
(20 − h − 16)(20 − h + 16) = 0 en utilisant l'identité remarquable a2 − b2 = (a − b)(a + b).
(4 − h)(36 − h) = 0 qui est une équation produit.
4 − h = 0 ou 36 − h = 0 car un produit est nul si et seulement si l'un de ses facteurs est nul.
h = 4 ou h = 36.
BC2 = AB2 + AC2
202 = 122 + (20 − h)2 en remplaçant les distances par leur expression ou valeurs.
(20 − h)2 = 400 − 144 = 256 = 162
(20 − h)2 − 162 = 0
(20 − h − 16)(20 − h + 16) = 0 en utilisant l'identité remarquable a2 − b2 = (a − b)(a + b).
(4 − h)(36 − h) = 0 qui est une équation produit.
4 − h = 0 ou 36 − h = 0 car un produit est nul si et seulement si l'un de ses facteurs est nul.
h = 4 ou h = 36.
La distance h est inférieure à 20, donc la seule solution qui convient est h = 4 pieds.
La longueur d'un pied est proche de 30 cm donc h 4 × 30 = 120 cm.
La longueur d'un pied est proche de 30 cm donc h
4 × 30 = 120 cm.
Nouveau message
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Centres étrangers, juin 2014, exercice 2
