Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 5
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 5
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 5
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 5
Énoncé
3 points
L'exercice suivant traite du thème « le canal du Midi »(1). Le vocabulaire spécifique est donné sur le schéma ci-dessous.
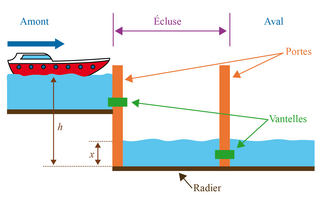 |
Pour une bonne partie de pêche au bord du canal, il faut un siège pliant adapté !
Nicolas est de taille moyenne et pour être bien assis, il est nécessaire que la hauteur de l'assise du siège soit comprise entre 44 cm et 46 cm.
Nicolas est de taille moyenne et pour être bien assis, il est nécessaire que la hauteur de l'assise du siège soit comprise entre 44 cm et 46 cm.
Voici les dimensions d'un siège pliable qu'il a trouvé en vente sur Internet :
- longueur des pieds : 56 cm ;
- largeur de l'assise : 34 cm ;
- profondeur de l'assise : 31 cm.
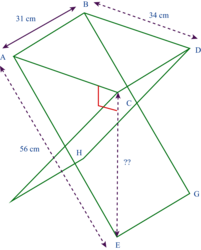 |
L'angle  est droit et ABCD est rectangle.
est droit et ABCD est rectangle.
La hauteur de ce siège lui est-elle adaptée ?
 est droit et ABCD est rectangle.
est droit et ABCD est rectangle.La hauteur de ce siège lui est-elle adaptée ?
Utilisez le théorème de Pythagore pour calculer la longueur CE.
(1)Le canal du Midi est un canal qui rejoint l'Atlantique à la Méditerranée.
Corrigé
Le quadrilatère ABCD est un rectangle donc AC = BD = 34 cm.
Le triangle ACE est rectangle en C, donc d'après le théorème de Pythagore :
AE2 = AC2 + CE2 soit CE2 = AE2 − AC2 = 562 − 342 = 3 136 − 1 156 = 1 980.
CE est un nombre positif car c'est une distance, donc CE =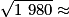 44,50 cm au centième près.
44,50 cm au centième près.
AE2 = AC2 + CE2 soit CE2 = AE2 − AC2 = 562 − 342 = 3 136 − 1 156 = 1 980.
CE est un nombre positif car c'est une distance, donc CE =
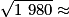 44,50 cm au centième près.
44,50 cm au centième près.On a 44  CE
CE  46 donc la hauteur de l'assise du siège est adaptée pour Nicolas.
46 donc la hauteur de l'assise du siège est adaptée pour Nicolas.
 CE
CE  46 donc la hauteur de l'assise du siège est adaptée pour Nicolas.
46 donc la hauteur de l'assise du siège est adaptée pour Nicolas.Corrigé
Le quadrilatère ABCD est un rectangle donc AC = BD = 34 cm.
Le triangle ACE est rectangle en C, donc d'après le théorème de Pythagore :
AE2 = AC2 + CE2 soit CE2 = AE2 − AC2 = 562 − 342 = 3 136 − 1 156 = 1 980.
CE est un nombre positif car c'est une distance, donc CE =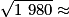 44,50 cm au centième près.
44,50 cm au centième près.
AE2 = AC2 + CE2 soit CE2 = AE2 − AC2 = 562 − 342 = 3 136 − 1 156 = 1 980.
CE est un nombre positif car c'est une distance, donc CE =
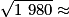 44,50 cm au centième près.
44,50 cm au centième près.On a 44  CE
CE  46 donc la hauteur de l'assise du siège est adaptée pour Nicolas.
46 donc la hauteur de l'assise du siège est adaptée pour Nicolas.
 CE
CE  46 donc la hauteur de l'assise du siège est adaptée pour Nicolas.
46 donc la hauteur de l'assise du siège est adaptée pour Nicolas.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 5
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 5
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 5
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 5

