Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 2
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 2
Énoncé
3 points
L'exercice suivant traite du thème « le canal du Midi »(1). Le vocabulaire spécifique est donné sur le schéma ci-dessous.
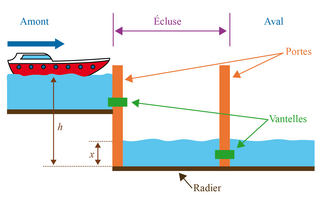 |
Pour amortir les chocs contre les autres embarcations ou le quai, les péniches sont équipées de « boudins » de protection.
Calculer le volume exact en cm3 du « boudin » de protection ci-dessous, puis arrondir au centième.
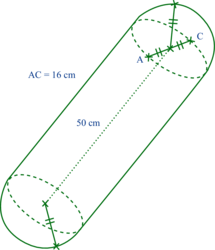 |
Rappel :
Volume d'un cylindre de révolution : V = πR2h
où h désigne la hauteur du cylindre et R le rayon de la base.
où h désigne la hauteur du cylindre et R le rayon de la base.
Volume d'une boule : V = 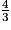 π R3
π R3
où R désigne le rayon de la boule.
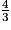 π R3
π R3où R désigne le rayon de la boule.
Remarquez que le « boudin » de protection est composé d'un cylindre de diamètre 16 cm et de hauteur 50 cm et de deux demi-boules de diamètre 16 cm.
(1)Le canal du Midi est un canal qui rejoint l'Atlantique à la Méditerranée.
Corrigé
Le volume du cylindre de diamètre AC = 16 cm, donc de rayon 8 cm, et de hauteur 50 cm est :
V1 = π × 82 × 50 = π × 64 × 50 = 3 200π cm3.
V1 = π × 82 × 50 = π × 64 × 50 = 3 200π cm3.
Le volume des deux demi-boules de diamètre AC = 16 cm, donc de rayon 8 cm est :
V2 =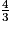 π × 83 =
π × 83 = 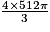 =
= 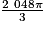 cm3.
cm3.
V2 =
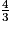 π × 83 =
π × 83 = 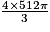 =
= 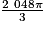 cm3.
cm3.Le volume exact du « boudin » de protection est donc :
V = V1 + V2 = 3 200π +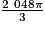 =
= 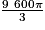 +
+ 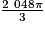 =
= 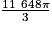 cm3.
cm3.
On a V 12 197,76 cm3 au centième près, en utilisant la touche « π » de la calculatrice.
12 197,76 cm3 au centième près, en utilisant la touche « π » de la calculatrice.
V = V1 + V2 = 3 200π +
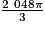 =
= 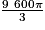 +
+ 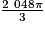 =
= 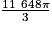 cm3.
cm3.On a V
 12 197,76 cm3 au centième près, en utilisant la touche « π » de la calculatrice.
12 197,76 cm3 au centième près, en utilisant la touche « π » de la calculatrice.Corrigé
Le volume du cylindre de diamètre AC = 16 cm, donc de rayon 8 cm, et de hauteur 50 cm est :
V1 = π × 82 × 50 = π × 64 × 50 = 3 200π cm3.
V1 = π × 82 × 50 = π × 64 × 50 = 3 200π cm3.
Le volume des deux demi-boules de diamètre AC = 16 cm, donc de rayon 8 cm est :
V2 =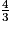 π × 83 =
π × 83 = 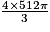 =
= 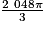 cm3.
cm3.
V2 =
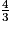 π × 83 =
π × 83 = 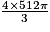 =
= 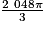 cm3.
cm3.Le volume exact du « boudin » de protection est donc :
V = V1 + V2 = 3 200π +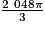 =
= 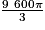 +
+ 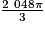 =
= 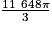 cm3.
cm3.
On a V 12 197,76 cm3 au centième près, en utilisant la touche « π » de la calculatrice.
12 197,76 cm3 au centième près, en utilisant la touche « π » de la calculatrice.
V = V1 + V2 = 3 200π +
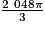 =
= 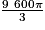 +
+ 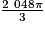 =
= 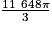 cm3.
cm3.On a V
 12 197,76 cm3 au centième près, en utilisant la touche « π » de la calculatrice.
12 197,76 cm3 au centième près, en utilisant la touche « π » de la calculatrice.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 2
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 2
Mathématiques - Travailler sur des sujets de brevet
Sujet Amérique du Nord, juin 2014, exercice 2

