Sujet de métropole, juin 2015, exercice 7

Énoncé

4 points

Ce panneau routier indique une descente dont la pente est de 10 %.

Cela signifie que pour un déplacement horizontal de 100 mètres, le dénivelé est de 10 mètres.
Le schéma ci-dessous n'est pas à l'échelle.

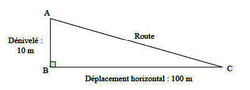1. Déterminer la mesure de l'angle $\widehat{\mathrm{BCA}}$ que fait la route avec l'horizontale. Arrondir la réponse au degré.

Utilisez une relation trigonométrique dans le triangle ABC rectangle en B. Vous devez trouver un angle compris entre 5 et 10°.

2. Dans certains pays, il arrive parfois que la pente d'une route ne soit pas donnée par un pourcentage, mais par une indication telle que « 1 : 5 », ce qui veut alors dire que pour un déplacement horizontal de 5 mètres, le dénivelé est de 1 mètre.
Lequel des deux panneaux ci-dessous indique la pente la plus forte ?

Pour les descentes représentées par les deux panneaux, déterminez le pourcentage de pente le plus élevé.

Voir le corrigé

Corrigé

Dans le triangle ABC rectangle en B, on a :
tan ( $\widehat{\mathrm{BCA}}$ ) = $\frac{\mathrm{AB}}{\mathrm{BC}}$ = $\frac{10}{100}$ = 0,1.
En utilisant la calculatrice (en mode degré) : $\widehat{\mathrm{BCA}}$ = tan⁻¹(0,1) $\approx 6^{\circ}$ au degré près.

Pour le panneau A, la pente est de 15 % et, pour le panneau B, la pente est de 100 × $\frac{1}{5}$ = 20 %.
C'est donc le panneau B qui indique la pente la plus forte.