Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Inde, avril 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet Inde, avril 2014, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Inde, avril 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet Inde, avril 2014, exercice 4
Énoncé
7 points
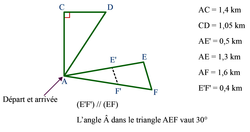
Une commune souhaite aménager des parcours de santé sur son territoire. On fait deux propositions au conseil municipal, schématisés ci-dessous :
Pouvez-vous les aider à choisir le parcours ? Justifier votre réponse.
Attention: la figure proposée au conseil municipal n'est pas à l'échelle, mais les codages et les dimensions données sont correctes.
- le parcours ACDA ;
- le parcours AEFA.
Pouvez-vous les aider à choisir le parcours ? Justifier votre réponse.
Attention: la figure proposée au conseil municipal n'est pas à l'échelle, mais les codages et les dimensions données sont correctes.
 |
Remarquez que le triangle AEF n'est pas forcément rectangle, donc que l'on ne peut pas utiliser les relations trigonométriques dans ce triangle.
Corrigé
Le parcours ACDA a pour longueur AC + CD + DA.
Les longueurs AC = 1,4 km et CD = 1,05 km sont connues et il reste à calculer la longueur DA.
Les longueurs AC = 1,4 km et CD = 1,05 km sont connues et il reste à calculer la longueur DA.
Le triangle ACD est rectangle en C, donc d'après le théorème de Pythagore :
DA2 = AC2 + CD2 = 1,42 + 1,052 = 1,96 + 1,1025 = 3,0625, donc DA =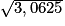 = 1,75 km.
= 1,75 km.
DA2 = AC2 + CD2 = 1,42 + 1,052 = 1,96 + 1,1025 = 3,0625, donc DA =
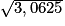 = 1,75 km.
= 1,75 km.Le parcours ACDA a donc pour longueur AC + CD + DA = 1,4 + 1,05 + 1,75 = 4,2 km.
Le parcours AEFA a pour longueur AE + EF + AF.
Les longueurs AE = 1,3 km et AF = 1,6 km sont connues et il reste à calculer la longueur EF.
Les longueurs AE = 1,3 km et AF = 1,6 km sont connues et il reste à calculer la longueur EF.
Dans le triangle AEF, E'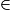 [AE], F'
[AE], F'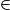 [AF] et les droites (EF) et (E'F') sont parallèles.
[AF] et les droites (EF) et (E'F') sont parallèles.
Donc, d'après le théorème de Thalès :
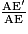 =
= 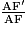 =
= 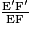 , donc en particulier
, donc en particulier 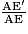 =
= 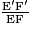 .
.
AE' = 0,5 km, AE = 1,3 km et E'F' = 0,4 km donc :
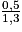 =
= 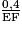 puis :
puis :
0,5 × EF = 1,3 × 0,4 = 0,52 et :
EF =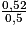 = 1,04 km.
= 1,04 km.
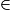 [AE], F'
[AE], F'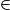 [AF] et les droites (EF) et (E'F') sont parallèles.
[AF] et les droites (EF) et (E'F') sont parallèles.Donc, d'après le théorème de Thalès :
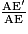 =
= 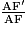 =
= 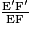 , donc en particulier
, donc en particulier 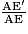 =
= 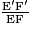 .
.AE' = 0,5 km, AE = 1,3 km et E'F' = 0,4 km donc :
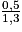 =
= 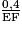 puis :
puis :0,5 × EF = 1,3 × 0,4 = 0,52 et :
EF =
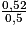 = 1,04 km.
= 1,04 km.Le parcours AEFA a donc pour longueur AE + EF + AF = 1,3 + 1,04 + 1,6 = 3,94 km.
4,2 − 4 = 0,2 > 0,06 = 4 − 3,94.
Le parcours dont la longueur s'approche le plus possible de 4 km est donc le parcours AEFA qui a pour longueur 3,94 km.
Le parcours dont la longueur s'approche le plus possible de 4 km est donc le parcours AEFA qui a pour longueur 3,94 km.
Corrigé
Le parcours ACDA a pour longueur AC + CD + DA.
Les longueurs AC = 1,4 km et CD = 1,05 km sont connues et il reste à calculer la longueur DA.
Les longueurs AC = 1,4 km et CD = 1,05 km sont connues et il reste à calculer la longueur DA.
Le triangle ACD est rectangle en C, donc d'après le théorème de Pythagore :
DA2 = AC2 + CD2 = 1,42 + 1,052 = 1,96 + 1,1025 = 3,0625, donc DA =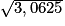 = 1,75 km.
= 1,75 km.
DA2 = AC2 + CD2 = 1,42 + 1,052 = 1,96 + 1,1025 = 3,0625, donc DA =
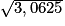 = 1,75 km.
= 1,75 km.Le parcours ACDA a donc pour longueur AC + CD + DA = 1,4 + 1,05 + 1,75 = 4,2 km.
Le parcours AEFA a pour longueur AE + EF + AF.
Les longueurs AE = 1,3 km et AF = 1,6 km sont connues et il reste à calculer la longueur EF.
Les longueurs AE = 1,3 km et AF = 1,6 km sont connues et il reste à calculer la longueur EF.
Dans le triangle AEF, E'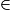 [AE], F'
[AE], F'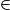 [AF] et les droites (EF) et (E'F') sont parallèles.
[AF] et les droites (EF) et (E'F') sont parallèles.
Donc, d'après le théorème de Thalès :
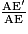 =
= 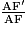 =
= 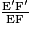 , donc en particulier
, donc en particulier 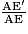 =
= 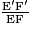 .
.
AE' = 0,5 km, AE = 1,3 km et E'F' = 0,4 km donc :
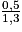 =
= 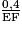 puis :
puis :
0,5 × EF = 1,3 × 0,4 = 0,52 et :
EF =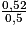 = 1,04 km.
= 1,04 km.
 [AE], F'
[AE], F'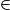 [AF] et les droites (EF) et (E'F') sont parallèles.
[AF] et les droites (EF) et (E'F') sont parallèles.Donc, d'après le théorème de Thalès :
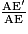 =
= 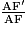 =
= 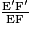 , donc en particulier
, donc en particulier 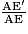 =
= 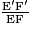 .
.AE' = 0,5 km, AE = 1,3 km et E'F' = 0,4 km donc :
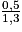 =
= 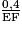 puis :
puis :0,5 × EF = 1,3 × 0,4 = 0,52 et :
EF =
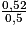 = 1,04 km.
= 1,04 km.Le parcours AEFA a donc pour longueur AE + EF + AF = 1,3 + 1,04 + 1,6 = 3,94 km.
4,2 − 4 = 0,2 > 0,06 = 4 − 3,94.
Le parcours dont la longueur s'approche le plus possible de 4 km est donc le parcours AEFA qui a pour longueur 3,94 km.
Le parcours dont la longueur s'approche le plus possible de 4 km est donc le parcours AEFA qui a pour longueur 3,94 km.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet Inde, avril 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet Inde, avril 2014, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet Inde, avril 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet Inde, avril 2014, exercice 4

