Énoncé
8 points
Pense-bête : toutes les formules données ci-dessous correspondent bien à des formules d'aires ou de volumes. On ne sait pas à quoi elles correspondent, mais elles peuvent quand même être utiles pour résoudre l'exercice ci-dessous.
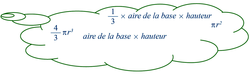 |
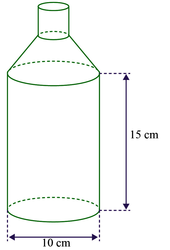
Voici une bouteille constituée d'un cylindre et d'un tronc de cône surmonté par un goulot cylindrique. La bouteille est pleine lorsque elle est remplie jusqu'au goulot.
Les dimensions sont notées sur le schéma.
Les dimensions sont notées sur le schéma.
 |
1.
Calculer le volume exact de la partie cylindrique de la bouteille, puis en donner un arrondi au cm3.
Rappelez-vous de la formule donnant le volume d'un cylindre en fonction du rayon R de sa base et de sa hauteur h.
Faites attention car 10 cm est le diamètre de sa base et non son rayon.
Faites attention car 10 cm est le diamètre de sa base et non son rayon.
2.
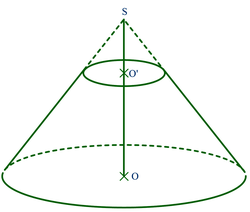
Pour obtenir le tronc de cône, on a coupé un cône par un plan parallèle à la base passant par O'. La hauteur SO du grand cône est de 6 cm et la hauteur SO' du petit cône est égale à 2 cm. Le rayon de la base du grand cône est de 5 cm.
 |
a)
Calculer le volume V1 du grand cône de hauteur SO (donner la valeur exacte).
Rappelez-vous que la formule donnant le volume d'un cône en fonction du rayon R de sa base et de sa hauteur h est 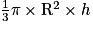 .
.
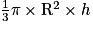 .
.b)
Montrer que le volume V2 du tronc de cône est égal à 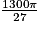 cm3. En donner une valeur arrondie au cm3.
cm3. En donner une valeur arrondie au cm3.
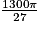 cm3. En donner une valeur arrondie au cm3.
cm3. En donner une valeur arrondie au cm3.Commencez par calculer le volume du petit cône qui est une réduction du grand cône.
Quel effet une réduction de rapport k a-t-elle sur les volumes ?
Quel effet une réduction de rapport k a-t-elle sur les volumes ?
3.
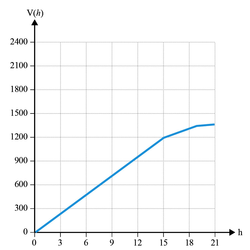
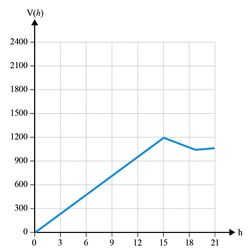
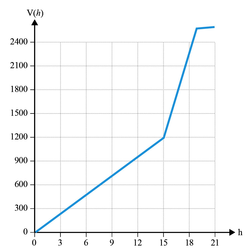
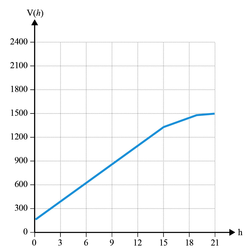
Parmi les quatre graphiques ci-après, l'un d'entre eux représente le volume V(h) de la bouteille en fonction de la hauteur h de remplissage du bidon.
Quel est ce graphique ? Pourquoi les autres ne sont-ils pas convenables ?
Quel est ce graphique ? Pourquoi les autres ne sont-ils pas convenables ?
 |
 |
 |
 |
Imaginez le remplissage du bidon successivement dans chacun des trois solides.
Corrigé
1.
Le volume d'un cylindre en fonction du rayon R de sa base et de sa hauteur h est 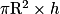 .
.
Ici, R =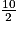 = 5 cm et h = 15 cm donc le volume de ce cylindre est :
= 5 cm et h = 15 cm donc le volume de ce cylindre est :
V = π × 52 × 15 = 25 × 15π = 375π 1 178 cm3 (arrondi à l'unité).
1 178 cm3 (arrondi à l'unité).
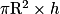 .
.Ici, R =
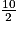 = 5 cm et h = 15 cm donc le volume de ce cylindre est :
= 5 cm et h = 15 cm donc le volume de ce cylindre est :V = π × 52 × 15 = 25 × 15π = 375π
 1 178 cm3 (arrondi à l'unité).
1 178 cm3 (arrondi à l'unité).2.
a) Le volume d'un cône en fonction du rayon R de sa base et de sa hauteur h est 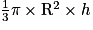 .
.
Ici, R = 5 cm et h = SO = 6 cm donc le volume du grand cône est :
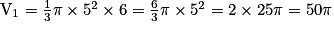 cm3.
cm3.
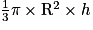 .
.Ici, R = 5 cm et h = SO = 6 cm donc le volume du grand cône est :
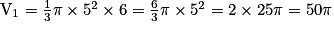 cm3.
cm3.b)
Calculons tout d'abord le volume du petit cône qui est une réduction de rapport 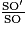 =
= 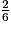 =
= 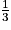 du grand cône.
du grand cône.
Une réduction de rapport k =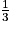 multiplie les volumes par k3 =
multiplie les volumes par k3 = 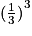 =
= 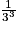 =
= 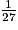 donc le volume du petit est
donc le volume du petit est 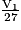 =
= 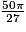 cm3.
cm3.
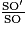 =
= 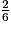 =
= 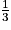 du grand cône.
du grand cône.Une réduction de rapport k =
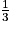 multiplie les volumes par k3 =
multiplie les volumes par k3 = 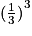 =
= 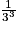 =
= 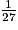 donc le volume du petit est
donc le volume du petit est 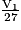 =
= 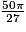 cm3.
cm3.Le volume V2 du tronc de cône est donc :
V2 = V1 −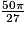
V2 = 50π −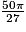
V2 = (1 − ) × 50π
) × 50π
V2 = (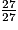 −
− 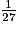 ) × 50π
) × 50π
V2 =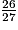 × 50π
× 50π
V2 =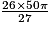
V2 =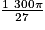 cm3.
cm3.
V2 151 cm3 (arrondi à l'unité).
151 cm3 (arrondi à l'unité).
V2 = V1 −
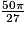
V2 = 50π −
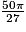
V2 = (1 −
 ) × 50π
) × 50πV2 = (
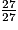 −
− 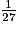 ) × 50π
) × 50πV2 =
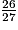 × 50π
× 50πV2 =
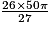
V2 =
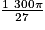 cm3.
cm3.V2
 151 cm3 (arrondi à l'unité).
151 cm3 (arrondi à l'unité).3.
Lorsque la valeur h de remplissage du bidon est comprise entre 0 et 15 cm, V(h)= = πR2 × h qui est une fonction linéaire de variable h.
La première portion de courbe est donc une droite passant par l'origine du repère.
Le graphique 4 est donc exclu.
La première portion de courbe est donc une droite passant par l'origine du repère.
Le graphique 4 est donc exclu.
Ensuite, lorsque le remplissage du bidon se fait dans le tronc du cône, le remplissage se fait un peu moins vite puis, dans le goulot cylindrique, le remplissage se fait de nouveau un peu moins vite.
Les pentes des portions de droite qui représentent le remplissage du bidon sont donc à chaque fois plus petite, tout en étant positive.
Les graphiques 3 et 2 sont donc exclus.
Les pentes des portions de droite qui représentent le remplissage du bidon sont donc à chaque fois plus petite, tout en étant positive.
Les graphiques 3 et 2 sont donc exclus.
Le volume V(h) de la bouteille en fonction de la hauteur h de remplissage du bidon est donc représenté par le graphique 1.

