Énoncé
19 points
Un club de natation propose un après-midi découverte pour les enfants.
Un club de natation propose un après-midi découverte pour les enfants.
PARTIE A
La présidente du club veut offrir des petits sachets cadeaux tous identiques contenant des autocollants et des drapeaux avec le logo du club. Elle a acheté 330 autocollants et 132 drapeaux et veut tous les utiliser. Elle veut que, dans chaque sachet, il y ait exactement le même nombre d'autocollants et que, dans chaque sachet, il y ait exactement le même nombre de drapeaux.
1. Pourquoi n'est-il pas possible de faire 15 sachets ?
Il faut comprendre que, dans cette première question, il faut essayer de faire les 15 sachets demandés en partageant les autocollants et les drapeaux achetés, mais en faisant attention car ils ne peuvent pas être coupés en plusieurs morceaux.
2.
a.
Décomposer 330 et 132 en produits de facteurs premiers.
b. En déduire le plus grand nombre de sachets que la présidente pourra réaliser.
c. Dans ce cas, combien mettra-t-elle d'autocollants et de drapeaux dans chaque sachet ?
Cette deuxième question est largement décomposée pour vous aider dans la résolution. Il s'agit ici de manipuler l'arithmétique, et notamment la décomposition des nombres pour obtenir des groupes identiques et leur composition.
Laissez-vous guider par l'enchaînement des questions en vous appliquant sur la rédaction des calculs et des explications et en ne voulant pas faire dès le début les trois questions à la fois.
Laissez-vous guider par l'enchaînement des questions en vous appliquant sur la rédaction des calculs et des explications et en ne voulant pas faire dès le début les trois questions à la fois.
PARTIE B
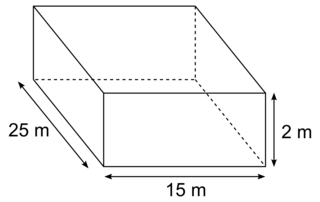
La piscine a la forme d'un pavé droit représenté ci-dessous.
Elle est remplie aux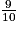
du volume.
1 m3 d'eau coûte 4,14 €.
Combien coûte le remplissage de la piscine ?
Elle est remplie aux
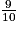du volume.1 m3 d'eau coûte 4,14 €.
Combien coûte le remplissage de la piscine ?
 |
Cette deuxième partie est à nouveau une question ouverte, mais qui n'est pas décomposée. Vous devez donc prendre le temps d'identifier chaque étape induite par la question pour les effectuer les unes après les autres en rédigeant complètement chaque calcul. Laissez-vous guider par l'enchaînement des informations et prenez votre temps, sur cette dernière question, pour ne pas la faire trop vite et passer à côté d'une information supplémentaire. Tout est relié à la proportionnalité, n'hésitez donc pas à vous appuyer sur des tableaux si nécessaire.
Corrigé
PARTIE A
1. On ne peut pas faire 15 sachets car même si les 330 autocollants peuvent être répartis en 15 sachets, les 132 drapeaux ne sont pas divisibles par 15. En effet : 330 ÷ 15 = 22 et 132 ÷ 15 = 8,8.
2.
a. On calcule les deux décompositions demandées (à la main ou à la calculatrice) et on obtient : 330 = 2 × 3 × 5 × 11 et 132 = 2 × 2 × 3 × 11.
b. Dans les deux décompositions obtenues à la question précédente, on observe que les diviseurs en commun sont 2, 3 et 11. On en conclut donc que le plus grand diviseur commun à 330 et 132 est : 2 × 3 × 11 = 66. On peut donc faire 66 sachets identiques au maximum.
c. On calcule enfin : 330 ÷ 66 = 5 et 132 ÷ 66 = 2 donc dans chacun des 66 sachets, elle pourra mettre 5 autocollants et 2 drapeaux.
PARTIE B
On calcule le volume de cette piscine : V=L × l × h = 25 × 15 × 2 = 750 m3.Ensuite, on veut la remplir aux
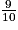donc on calcule : 
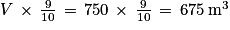.Enfin, on sait que 1 m3 coûte 4,14 €, on calcule donc : P = 675 × 4,14 = 2 794,50 €.
Le coût de remplissage de cette piscine est donc de 2 794,50 €.
