Déterminer une fonction affine à partir des images de deux nombres
Exemple
On veut déterminer la fonction affine f telle que 1 ait pour image –1 et 2 ait pour image 10.
f est de la forme f(x) = ax + b.
Il s'agit donc de déterminer a et b.
Il s'agit donc de déterminer a et b.
Méthode :
1 a pour image –1 entraîne f(1) = –1 donc a + b = –1.
2 a pour image 10 entraîne f(2) = 10 donc 2a + b = 10.
Lorsqu'on soustrait membre à membre les deux égalités, les coefficients b s'annulent.
On obtient a = 11.
On obtient a = 11.
En remplaçant a par 11 dans l'une des deux égalités, on obtient b = –12.
On a donc : f(x) = 11x – 12.
Remarque
On peut aussi déterminer une fonction affine à partir de sa représentation graphique : les coordonnées de deux points donnent les images de deux nombres.
Exercice n°1
On sait que : f(1) = -3 et f(-1) = 7.
Détermine la fonction affine f.
Détermine la fonction affine f.
Écrivez les réponses dans les zones colorées.
1. f est de la forme f(x) = ax + b.
Si f(1) = -3, alors : a × + b = .
Si f(-1) = 7, alors : a × () + b = .
Si f(1) = -3, alors : a × + b = .
Si f(-1) = 7, alors : a × () + b = .
2. On obtient : a = et b = .
1. f(1) = -3, donc a + b = -3.
f(-1) = 7, donc -a + b = 7.
f(-1) = 7, donc -a + b = 7.
2. Pour trouver a et b, il faut résoudre le système. Par addition membre à membre, on obtient 2b = 4, soit b = 2.
a + 2 = -3, soit a = -5.
a + 2 = -3, soit a = -5.
Exercice n°2
f est une fonction affine dont la représentation graphique est une droite d qui passe par les points A(0 ; 6) et B(1 ; 2).
Détermine l'expression de f.
Détermine l'expression de f.
Écrivez les réponses dans les zones colorées.
1. A appartient à d, donc f() = .
B appartient à d, donc f() = .
B appartient à d, donc f() = .
2. f est de la forme f(x) = ax + b.
Si f(0) = , alors b = .
Si f() = , alors a + b = .
Si f(0) = , alors b = .
Si f() = , alors a + b = .
3. On a donc : f(x) = x + .
• A(0 ; 6) donc f(0) = 6, soit b = 6.
B(1 ; 2) donc f(1) = 2, soit a + b = 2.
B(1 ; 2) donc f(1) = 2, soit a + b = 2.
• La seconde équation s'écrit a + 6 = 2, soit a = -4.
Alors f(x) = -4x + 6.
Alors f(x) = -4x + 6.
Exercice n°3
Les affirmations suivantes sont-elles vraies ou fausses ?
Coche la bonne réponse.
Coche la bonne réponse.
a. Pour déterminer la fonction affine f telle que f(−1) = 2 et f(2) = 1, on cherche a et b tels que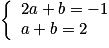 
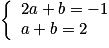
Cochez la bonne réponse.
| ||
|
b. Pour déterminer la fonction affine f telle que f(−2) = 1 et f(1) = 2, on cherche a et b tels que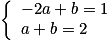 
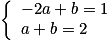
Cochez la bonne réponse.
| ||
|
c. On peut trouver plusieurs fonctions affines f telles que f(−1) = 2.
Cochez la bonne réponse.
| ||
|
a. Le système traduit f(2) = −1 et f(1) = 2.
c. Ces fonctions affines sont représentées par les droites non parallèles à l'axe des ordonnées, qui passent par A(−1 ; 2).
Exercice n°4
Complète le texte suivant pour déterminer la fonction affine telle que f(5) =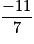 
et dont la représentation graphique passe par le point A (7 ; −1).
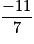et dont la représentation graphique passe par le point A (7 ; −1). Écrivez les réponses dans les zones colorées.
La représentation de la fonction f passe par le point A(7 ; −1) cela signifie que f(7) = or f est une fonction affine de la forme f(x) = .
Donc f(5) = −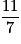
signifie a × + = −
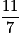et f(7) = −1 signifie a × + b = .
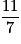signifie a × + = − 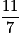et f(7) = −1 signifie a × + b = .D'où : a =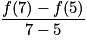 
= 
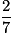et b = .
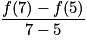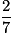= et b = .
