Problème
Un théâtre propose les formules suivantes :
- première formule : abonnement annuel de 10 € et 10 € par spectacle ;
- seconde formule : abonnement annuel de 40 €.
Mise en équation
Soit x le nombre de spectacles :
- la première formule correspond à la fonction affine f(x) = 10x + 10 ;
- la seconde formule correspond à la fonction affine g(x) = 40.
Résolution graphique
On représente f par la droite D d'équation y = 10x + 10 et g par la droite D' d'équation y = 40.
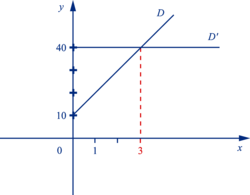 |
On en conclut qu'au-delà de trois places, la seconde formule est la plus avantageuse, car D' passe « au-dessous » de D.
Exercice n°1
Deux agences de location de voitures proposent les tarifs suivants :
- agence V : forfait 50 € et 0,50 € par km ;
- agence W : forfait 100 € et 0,25 € par km.
On veut déterminer graphiquement quel est le tarif le plus intéressant en fonction du nombre de km.
Suis les indications ci-dessous et complète la réponse.
Suis les indications ci-dessous et complète la réponse.
Écrivez les réponses dans les zones colorées.
1. On représente graphiquement, par deux droites V et W, le prix à payer à chaque agence en fonction du nombre x de km.
La droite V a pour équation : y = x + .
La droite W a pour équation : y =x + .
La droite V a pour équation : y = x + .
La droite W a pour équation : y =x + .
2. On lit sur le graphique que l'agence W offre un tarif plus intéressant au-delà de km.
1. Tu peux choisir l'échelle suivante : 1 cm pour 100 km en abscisse et 1 cm pour 50 € en ordonnée.
2. Sur la représentation graphique, les droites se coupent au point (200 ; 150). Après ce point, la droite W passe en dessous de la droite V.
Exercice n°2
Dans un théâtre municipal, deux options sont proposées :
- option A : 10 € par spectacle ;
- option B : un abonnement annuel de 30 € et 4 € par spectacle.
En utilisant un graphique, détermine à partir de combien de séances l'option B est plus avantageuse que l'option A pour un amateur de théâtre.
Écrivez la réponse dans la zone colorée.
Réponse : l'option B est plus avantageuse à partir de séances.
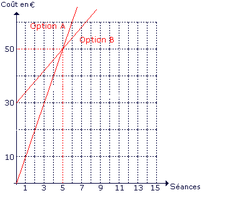 |
Exercice n°3
Un vidéo club propose deux formules :
- formule A : abonnement de 50 € puis 2 € par cassette louée ;
- formule B : abonnement de 20 € puis 4 € par cassette louée.
On veut déterminer graphiquement quelle est la formule la plus avantageuse en fonction du nombre de cassettes louées.
Suis les indications ci-dessous et complète la réponse.
Suis les indications ci-dessous et complète la réponse.
Écrivez les réponses dans les zones colorées.
a. On représente graphiquement, par deux droites A et B, le prix à payer en fonction du nombre x de cassettes louées :
→ la droite A a pour équation : y = x + .
→ la droite B a pour équation : y = x + .
→ la droite A a pour équation : y = x + .
→ la droite B a pour équation : y = x + .
b. On lit sur le graphique que la formule A est plus avantageuse au-delà de cassettes.
a. Tu peux choisir l'échelle suivante : 1 cm pour 5 cassettes en abscisse et 1 cm pour 10 € en ordonnée.
b. Sur la représentation graphique, les droites se coupent au point (15 ; 80). Après ce point, la droite A passe en dessous de la droite B.
Exercice n°4
Deux boutiques de location de déguisements proposent le même type de déguisements aux tarifs suivants :
– boutique n°1 : 25 € de réservation plus 0,21 € par heure de location ;
– boutique n°2 : 40 € de réservation plus 0,16 € par heure de location.
– boutique n°1 : 25 € de réservation plus 0,21 € par heure de location ;
– boutique n°2 : 40 € de réservation plus 0,16 € par heure de location.
En utilisant un graphique, détermine à partir de combien d'heures la boutique n°2 devient la plus avantageuse.
Écrivez la réponse dans la zone colorée.
La boutique n°2 est la plus avantageuse à partir de heures de location.
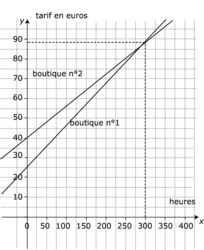 |

