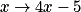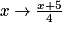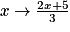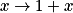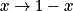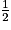Propriété
Dans un plan muni d'un repère (O ; I ; J), la représentation graphique de la fonction affine x → ax + b est la droite d'équation : y = ax + b.
a est le coefficient directeur de la droite et b est son ordonnée à l'origine.
Exemple
Soit la fonction affine f définie par f(x) = 2x – 1.
• Sa représentation graphique est une droite. Pour la tracer, deux points suffisent. On a f(−1) = −3 ; et f(1) = 3 donc les points A(−1 ; −3) et b(1 ; 1) appartiennent à D.
Cas particuliers
• On a f(x) = b.
La fonction f est constante : sa représentation graphique est une droite d'équation : y = b. Cette droite est parallèle à l'axe des abscisses.
• On a f(x) = ax.
La fonction f est linéaire : sa représentation graphique est une droite d'équation : y = ax, qui passe par l'origine du repère.
Exercice n°1
Soit f la fonction qui, à x, associe le nombre -5 + 4x.
Détermine l'équation de la droite D représentant f et les coordonnées de trois points de D.
Détermine l'équation de la droite D représentant f et les coordonnées de trois points de D.
Écrivez les réponses dans les zones colorées.
1. La droite D a pour équation : y = x .
2. Si x = 1, y = ; D passe donc par le point ( ; ).
3. Si y = 7, x = ; D passe donc par le point de coordonnées ( ; ).
4. La droite D passe aussi par le point de coordonnées (0 ; ).
1. D a pour équation : y = 4x − 5.
2. Si x = 1, alors y = 4 × 1 − 5.
Ce qui donne : y = -1.
Ce qui donne : y = -1.
3. Si y = 7, alors 7 = 4x − 5.
Ce qui donne :
12 = 4x
x = 3.
Ce qui donne :
12 = 4x
x = 3.
4. L'ordonnée à l'origine est -5.
Exercice n°2
 |
Soit trois fonctions affines f, g, et h telles que :
- f(x) = x + 2 ;
- g(x) = -x − 2 ;
- h(x) = -x + 2.
Écrivez les réponses dans les zones colorées.
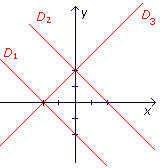
1. La droite D1 représente la fonction .
2. La droite D2 représente la fonction .
3. La droite D3 représente la fonction .
1. La pente de la droite D1 est telle que son coefficient directeur est négatif. En outre, elle passe par le point de coordonnées (0 ; -2). Son équation est donc y = -x − 2.
2. La droite D2 a aussi un coefficient directeur négatif.
Exercice n°3
La représentation graphique de la fonction affine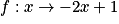 
est une droite qui passe par le point de coordonnées :
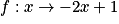est une droite qui passe par le point de coordonnées : Cochez la bonne réponse.
| ||
| ||
|
Soit A(2 ; 3) et B(−1 ; 1) ; les points A et B appartiennent à la représentation graphique de la fonction :
Cochez la bonne réponse.
| ||
| ||
|
Exercice n°4
 |
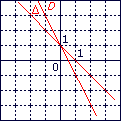Coche la bonne réponse.
La fonction affine qui est représentée par la droite Δ est :
Cochez la bonne réponse.
| ||
| ||
|
Si D représente la fonction affine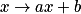 
, alors a est égal à :
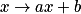, alors a est égal à : Cochez la bonne réponse.
| ||
| ||
|
