Exemple 1
Les tarifs d'un plombier sont : 25 € de l'heure de travail et 12 € pour le déplacement.
• Le prix payé par un client est une fonction affine du nombre d'heures de travail.
• Si l'on désigne par f(x) le prix payé par le client en fonction du nombre x d'heures, on a :
f(x) = 25x + 12.
f(x) = 25x + 12.
• Si le plombier travaille 2 heures chez M. Fuitdo, celui-ci lui doit :
f(2) = 25 × 2 + 12 = 62 ; soit 62 €.
f(2) = 25 × 2 + 12 = 62 ; soit 62 €.
Exemple 2
Un aquarium contient 120 l d'eau. Cette eau s'évapore à raison de 6 cl par heure.
Quelle quantité d'eau reste-t-il dans l'aquarium au bout de quatre jours ?
• La quantité d'eau qui reste est une fonction affine de la durée d'évaporation.
• Si l'on désigne par g(t) la quantité d'eau dans l'aquarium au bout du temps t (t en heures), on a :
g(t) = 120 – 0,06t.
g(t) = 120 – 0,06t.
• 4 jours = 4 × 24 heures = 96 heures.
g(96) = 120 – 0,06 × 96 = 114,24
g(96) = 120 – 0,06 × 96 = 114,24
Au bout de quatre jours, il reste environ 114 litres dans l'aquarium.
Exercice n°1
Un parc automobile pratique les tarifs suivants : 2 € de prise en charge pour chaque véhicule, plus 1,20 € de l'heure. Une heure commencée est due.
Détermine la fonction affine associée à cette situation et utilise-la.
Détermine la fonction affine associée à cette situation et utilise-la.
Écrivez les réponses dans les zones colorées.
1. Si l'on désigne par f(x) la somme à payer en fonction du nombre x d'heures, on a :
f(x) = x + .
f(x) = x + .
2. Jean reste 45 min : il payera €. Léa reste 3 heures : elle payera €.
2. Attention, toute heure commencée est due.
1. 2 € de prise en charge plus 1,20 € par heure :
f(x) = 1,20x + 2.
f(x) = 1,20x + 2.
2. Une heure commencée est due. Jean reste 45 min, mais paye pour 1 h.
f(1) = 1,20 × 1 + 2 = 3,20.
f(3) = 1,20 × 3 + 2 = 5,60.
f(1) = 1,20 × 1 + 2 = 3,20.
f(3) = 1,20 × 3 + 2 = 5,60.
Exercice n°2
Un vidéo club propose trois formules :
- formule A : abonnement de 50 €, puis 2 € par cassette louée ;
- formule B : abonnement de 25 €, puis 4 € par cassette louée ;
- formule C : 5,50 € par cassette louée.
Détermine la fonction affine qui exprime le prix à payer en fonction du nombre x de cassettes.
Écrivez les réponses dans les zones colorées.
1. Avec la formule A : f(x) = x + .
2. Avec la formule B : g(x) = x + .
3. Avec la formule C : h(x) = x.
1. Formule A : 50 €, puis 2 € par cassette.
f(x) = 50 + 2x.
f(x) = 50 + 2x.
2. Formule B : 25 €, puis 4 € par cassette.
g(x) = 25 + 4x.
g(x) = 25 + 4x.
3. Formule C : 5,50 € par cassette sans abonnement.
h(x) = 5,50x.
h(x) = 5,50x.
Exercice n°3
Un commerçant décide d'augmenter tous les prix.
On note f(x) le prix en € d'un article qui coûtait x €.
On note f(x) le prix en € d'un article qui coûtait x €.
Les affirmations suivantes sont-elles vraies ou fausses ?
Coche la bonne réponse.
Coche la bonne réponse.
a. Il décide que chaque prix doit être augmenté de 10 € ; on a alors : f(x) = x + 10.
Cochez la bonne réponse.
| ||
|
b. Il décide que chaque prix doit être augmenté de 10 % ; on a alors : f(x) = x + 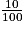
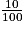
Cochez la bonne réponse.
| ||
|
b. Dans ce cas, on a : f(x) = 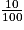 x, donc f(x) = x(1 + 0,1) ; d'où f(x) = 1,1x.
x, donc f(x) = x(1 + 0,1) ; d'où f(x) = 1,1x.
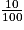 x, donc f(x) = x(1 + 0,1) ; d'où f(x) = 1,1x.
x, donc f(x) = x(1 + 0,1) ; d'où f(x) = 1,1x.Exercice n°4
Dans chacune des situations suivantes, exprime y en fonction de x.
Écrivez les réponses dans les zones colorées.
a. Le tarif d'un dépanneur en électroménager est : 31,50 € de l'heure, plus 17 € pour le déplacement.
y est le montant, en €, que doit payer un client chez lequel ce dépanneur a effectué x heures de travail.
y =
y est le montant, en €, que doit payer un client chez lequel ce dépanneur a effectué x heures de travail.
y =
b. L'agence Belloto propose la location d'un véhicule au tarif suivant : 55 € de forfait, plus 0,25 € au kilomètre parcouru.
y est le montant, en €, à payer par un client qui a parcouru x kilomètres.
y =
y est le montant, en €, à payer par un client qui a parcouru x kilomètres.
y =

