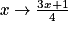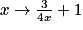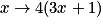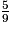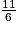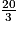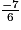Définition
Étant donné deux nombres a et b, le procédé de calcul qui, à tout nombre x, associe le nombre ax + b est une fonction affine.
Notation
En général, on désigne une fonction par les lettres f, g ou h.
On écrit f : x → ax + b
ou, plus souvent, f(x) = ax + b.
ou, plus souvent, f(x) = ax + b.
Ces notations signifient : l'image de x par la fonction f est ax + b.
Exemples
• Soit f : x → 2x – 5 ;
On veut calculer l'image du nombre 1 par f.
2 × 1 – 5 = –3 ; on écrit : f(1) = –3.
• On a :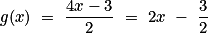 
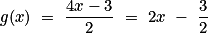
g est une fonction affine avec a = 2 et b = –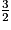 
.
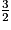.Cas particuliers
• Si b = 0, on obtient la fonction linéaire : x → ax.
• Si a = 0, on obtient la fonction constante : x → b.
Exercice n°1
Complète avec les nombres qui conviennent.
Écrivez les réponses dans les zones colorées.
1. Soit f(x) = -4x.
f(-1) =
f(0) =
f(3) =
f(-1) =
f(0) =
f(3) =
2. Soit g(x) = -3x + 4.
g(-1) =
g(0) =
g(3) =
g(-1) =
g(0) =
g(3) =
3. Soit h(x) = 6.
h(-1) =
h(0) =
h(3) =
h(-1) =
h(0) =
h(3) =
1. f(x) = -4x
f(-1) = -4x − 1 = 4
f(-1) = -4x − 1 = 4
2. g(x) = -3x + 4
g(-1) = -3x − 1 + 4 = 7
g(-1) = -3x − 1 + 4 = 7
3. h(x) = 6.
Le résultat ne dépend donc pas de la valeur de x. C'est toujours 6.
Le résultat ne dépend donc pas de la valeur de x. C'est toujours 6.
Exercice n°2
La fonction est-elle affine ? Réponds par oui ou par non. Puis détermine, le cas échéant, les valeurs de son coefficient directeur a et de son ordonnée à l'origine b.
Écrivez les réponses dans les zones colorées.
1. f(x) = x − 4x(x + 3) + 2x
f est-elle une fonction affine ?
f est-elle une fonction affine ?
2. g(x) = (2x − 1) − 4(x + 1)
g est-elle une fonction affine ?
a =
b =
g est-elle une fonction affine ?
a =
b =
1. f(x) = x − 4x(x + 3) + 2x
f(x) = -4x2 − 9x
L'expression comporte un terme « en x2 » : f n'est pas affine.
f(x) = -4x2 − 9x
L'expression comporte un terme « en x2 » : f n'est pas affine.
2. g(x) = (2x − 1) − 4(x + 1)
g(x) = -2x − 5
g est de la forme ax + b avec a = -2 et b = -5.
g(x) = -2x − 5
g est de la forme ax + b avec a = -2 et b = -5.
Exercice n°3
Coche la bonne réponse.
Parmi les fonctions suivantes, laquelle n'est pas une fonction affine ?
Cochez la bonne réponse.
| ||
| ||
|
Soit f l'application affine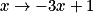 
; alors f(−
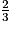) est égal à :
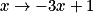; alors f(−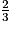) est égal à : Cochez la bonne réponse.
| ||
| ||
|
Le nombre qui a pour image −3 par la fonction affine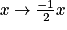 
+ 
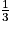
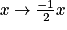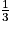
+ Cochez la bonne réponse.
| ||
| ||
|
Une fonction affine associe, à chaque nombre x, le nombre ax + b.
Exercice n°4
Soit la fonction affine f définie par f(x) = −7x + 3. Complète la démonstration suivante :
Écrivez les réponses dans les zones colorées.
Pour a = 2 et b = 3 on a : f(a) = −7 × 2 + 3 = et f(b) = −7 × 3 + 3 = .
f(a) − f(b) = = .
Or −7(a − b) = −7(2 − 3) = −7 × (−1) = 7.
On constate que f(a) − f(b) = .
