Déterminer une fonction linéaire à partir d'un nombre et de son image
Exemple
f est la fonction linéaire telle que –12 a pour image 28.
Déterminer f.
Déterminer f.
• f étant définie par une relation de la forme f(x) = ax, il s'agit de calculer a.
• f(–12) = 28 ; donc a× (–12) = 28, on obtient alors :
a =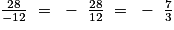 .
.
a =
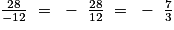 .
.• Conclusion : f est définie par f(x) = – 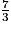 x.
x.
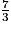 x.
x.Remarque
On peut aussi déterminer une fonction linéaire à partir de la droite D qui la représente graphiquement :
les coordonnées (x ; y) d'un point de D correspondent à un nombre, x, et à son image, y, par la fonction.
les coordonnées (x ; y) d'un point de D correspondent à un nombre, x, et à son image, y, par la fonction.
Exercice n°1
Une fonction linéaire f est telle que f(-3) = 18.
Détermine la fonction f, puis calcule les images de quatre nombres.
Détermine la fonction f, puis calcule les images de quatre nombres.
Écrivez les réponses dans les zones colorées.
1. f est de la forme f(x) = ax.
f(-3) = 18, donc a × () = , soit a = .
f(-3) = 18, donc a × () = , soit a = .
2. On en déduit :
f(-1) =
f(2) =
f(-4) =
f(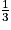 ) =
) =
f(-1) =
f(2) =
f(-4) =
f(
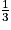 ) =
) = 1. f(-3) = 18 donc a × (-3) = 18, soit a = -6.
2. f(-1) = -6 × (-1)
f(2) = -6 × 2
f(-4) = -6 × (-4)
f(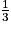 ) = -6 ×
) = -6 × 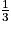 .
.
f(2) = -6 × 2
f(-4) = -6 × (-4)
f(
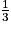 ) = -6 ×
) = -6 × 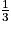 .
. Exercice n°2
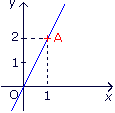 |
La droite D est la représentation graphique d'une fonction linéaire f.
Détermine la fonction f à partir des coordonnées du point A.
Détermine la fonction f à partir des coordonnées du point A.
Écrivez les réponses dans les zones colorées.
1. D'après la lecture du graphique :
f() = .
f() = .
2. On en déduit que :
f(x) = x.
f(x) = x.
1. A de coordonnées (1 ; 2) est un point de la droite D, donc f(1) = 2.
2. f est une application linéaire, donc f(x) = a × x.
Ainsi 2 = a × 1, soit a = 2.
Ainsi 2 = a × 1, soit a = 2.
Exercice n°3
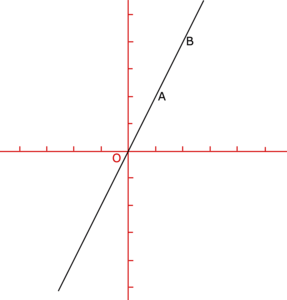
Quelle est la fonction linéaire ayant pour représentation la droite (AB) ?
 |
Cochez la bonne réponse.
| ||
| ||
| ||
|
• Le point A a pour coordonnées (1 ; 2), donc f(1) = 2. Divise l'image par son antécédent pour calculer le coefficient. Il est égal à 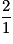 = 2.
= 2.
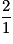 = 2.
= 2.• La fonction f est définie par f(x) = 2x.

