Définition d'une rotation
Une rotation est définie par un point O du plan et un angle orienté de mesure 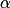 (le sens inverse des aiguilles d’une montre est appelé sens direct).
(le sens inverse des aiguilles d’une montre est appelé sens direct).
Le point A' image du point A par cette rotation est tel que OA' = OA et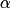 =
= 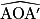 , où les deux angles ont la même orientation.
, où les deux angles ont la même orientation.
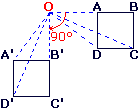
Sur la figure ci-dessous,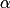 = 75° et le sens de la rotation est le sens direct.
= 75° et le sens de la rotation est le sens direct.
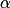 (le sens inverse des aiguilles d’une montre est appelé sens direct).
(le sens inverse des aiguilles d’une montre est appelé sens direct). Le point A' image du point A par cette rotation est tel que OA' = OA et
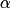 =
= 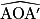 , où les deux angles ont la même orientation.
, où les deux angles ont la même orientation. Sur la figure ci-dessous,
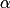 = 75° et le sens de la rotation est le sens direct.
= 75° et le sens de la rotation est le sens direct.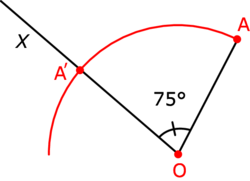 |
Propriétés d'une rotation
- Une rotation conserve l'alignement, les longueurs, le parallélisme, les angles et les aires .
- Par une rotation, l'image d'un cercle est un cercle de même rayon.
Construction de l'image d'une figure par une rotation
Pour construire l'image d'une figure simple par rotation, il suffit de construire l'image de chacun de ses points caractéristiques.
Exemple
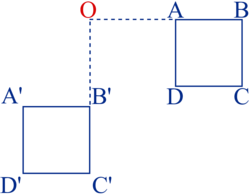
A'B'C'D' est l'image de ABCD par la rotation de centre O et d'angle 90°, en sens indirect (le sens des aiguilles d'une montre).
 |
On remarque que ABCD et A'B'C'D' sont superposables.
 |
Exercice n°1
On veut représenter F et son image par une rotation de centre I et d'angle 90°, en sens indirect.
Sélectionne la figure qui correspond.
Sélectionne la figure qui correspond.
| ||
| Figure 1 |
| ||
| Figure 2 |
| ||
| Figure 3 |
• Dans la figure 1, on a effectué une symétrie de centre I, donc une rotation de 180°.
• Dans la figure 2, on a effectué une symétrie par rapport à une droite passant par le point I.
Exercice n°2
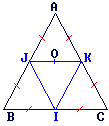 |
ABC est un triangle équilatéral.
I, J, K sont les milieux des côtés de ABC.
Complète la description des deux rotations suivantes.
I, J, K sont les milieux des côtés de ABC.
Complète la description des deux rotations suivantes.
Écrivez les réponses dans les zones colorées.
1. Par la rotation de centre et d'angle °, IJK devient AKJ.
2. Par la rotation de centre et d'angle 60° en sens direct, IKJ devient I.
1. IJK devient AKJ par une symétrie de centre O, donc une rotation de 180°.
2. I est invariant : c'est le centre de la rotation.
Le sens direct est le sens contraire des aiguilles d'une montre.
Le sens direct est le sens contraire des aiguilles d'une montre.
Exercice n°3
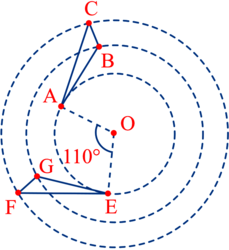 |
Le triangle EGF est l'image du triangle ABC par la rotation de centre O et d'angle 110° dans le sens direct.
Complète les phrases suivantes.
Complète les phrases suivantes.
Écrivez les réponses dans les zones colorées.
a. Par cette rotation de 110° dans le sens direct et de centre O :
- l'image de A est : ;
- l'image de B est : ;
- l'image de C est : ;
- l'image du triangle ABC est : .
Pour construire l'image du triangle ABC par la rotation de centre O et d'angle 110° dans le sens direct, on construit l'image de chaque sommet par cette rotation.
L'image d'une figure par rotation est superposable à la figure initiale, une rotation conserve les longueurs, les alignements et les angles.