L'image d'une droite par une translation
• Une translation transforme une droite d en une droite d' parallèle à D.
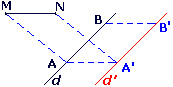 |
• Pour construire d, on peut :
- soit construire les images de deux points distincts de la droite d;
- soit tracer la parallèle à d passant par l'image d'un point de d.
Autres propriétés
• Une translation conserve les distances, les angles, et les aires.
• L'image d'un cercle par une translation est un cercle de même rayon.
Exercice n°1
On veut construire d', l'image d'une droite d par la translation qui transforme M en N.
Complète les consignes.
Complète les consignes.
Écrivez les réponses dans les zones colorées.
1. On place un point A sur d.
2. On trace la à (MN) passant par A.
3. On place B sur cette droite tel que AB = , en respectant le sens du glissement.
4. d' est la à d passant par .
Une droite et son image par translation sont parallèles.
Il suffit donc de construire l'image d'un point de d et de tracer la parallèle passant par ce point.
Il suffit donc de construire l'image d'un point de d et de tracer la parallèle passant par ce point.
Exercice n°2
R, T et U sont trois points non alignés.
Complète ces trois phrases.
Complète ces trois phrases.
Écrivez les réponses dans les zones colorées.
1. L'image de R par la translation qui transforme T en U est le point S tel que RS soit un parallélogramme.
2. L'image du segment [RT] par la translation qui transforme T en U est le segment [] et on a RT = .
3. Par cette même translation, l'image de la droite (TS) est la droite qui passe par .
Par la translation qui transforme T en U, l'image de R est le point S tel que (RS) // (TU) et RS = TU.
Donc RSUT est un parallélogramme.
Donc RSUT est un parallélogramme.
Exercice n°3
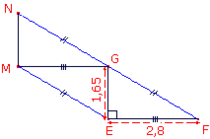 |
N, G et F sont alignés.
Réponds aux questions suivantes ?
Écrivez les réponses dans les zones colorées.
a. Quelle est l'image du point E par la translation qui transforme F en G ?
b. Quelle est l'image du point G par la translation qui transforme F en G ?
c. Quelle est l'image du segment [EG] par la translation qui transforme F en G ?
d. Combien mesure le périmètre du quadrilatère EMNF ? (Calcule d'abord GF.) cm.
a. Les côtés opposés du quadrilatère EMGF ayant la même longueur, EMGF est un parallélogramme ; l'image de E par la translation qui transforme F en G est donc M.
c. L'image d'un segment par une translation est un segment parallèle et de même longueur.
On en déduit que MN = EG = 1,65 cm ; ce résultat va être utilisé dans le calcul du périmètre.
On en déduit que MN = EG = 1,65 cm ; ce résultat va être utilisé dans le calcul du périmètre.
d. EFG est un triangle rectangle en E, on calcule GF à l'aide du théorème de Pythagore.
On obtient GF = 3,25 cm.
Le périmètre de EMNF est égal à : EM + MN + NG + GF + FE donc à 3,25 + 1,65 + 3,25 + 3,25 + 2,8.
On obtient GF = 3,25 cm.
Le périmètre de EMNF est égal à : EM + MN + NG + GF + FE donc à 3,25 + 1,65 + 3,25 + 3,25 + 2,8.
Exercice n°4
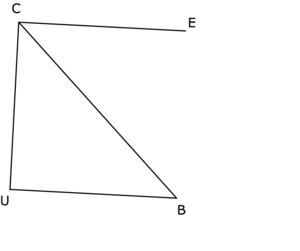
CUB est un triangle rectangle et isocèle en U. Par la translation qui transforme U en B, C a pour image E. Quelle est la nature du quadrilatère CUBE ?
Cochez la bonne réponse.
| ||
| ||
| ||
| ||
|
Trace une figure à main levée pour t'aider.
• Par la translation qui transforme U en B, C a pour image E, donc le quadrilatère CUBE est un parallélogramme.
• De plus, UB = UC et les droites (UB) et (UC) sont perpendiculaires.
Le parallélogramme possède un angle droit et deux côtés consécutifs égaux, c'est un carré.
Le parallélogramme possède un angle droit et deux côtés consécutifs égaux, c'est un carré.
 |

