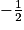Définition d'une homothétie
L'image M' du point M du plan par une homothétie de centre O et de rapport k (non nul) est défini par :- OM' = k×OM ;
- si k > 0, M'
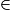 [OM) (M et M' sont du même côté par rapport à O) ;
[OM) (M et M' sont du même côté par rapport à O) ; - si k < 0, M'
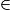 [MO) (M et M' sont de part et d'autre de O).
[MO) (M et M' sont de part et d'autre de O).
 |
Le point M' est l'image du point M par l'homothétie de centre O et de rapport −2.
Propriétés d'une homothétie
- L'homothétie de centre O et de rapport −1 est la symétrie de centre O.
- Une homothétie conserve l'alignement, le parallélisme et les angles.
- Une homothétie multiplie les longueurs par
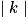 : si
: si 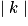 > 1, l'image d'une figure est un agrandissement de cette figure et, si
> 1, l'image d'une figure est un agrandissement de cette figure et, si 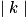 < 1, l'image d'une figure est une réduction de cette figure.
< 1, l'image d'une figure est une réduction de cette figure. - Une homothétie de rapport k transforme un segment [AB] en un segment de longueur
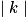 AB.
AB. - Une homothétie de rapport k multiplie les aires par k2.
Lien avec le théorème de Thalès
Soit h l'homothétie de centre A et de rapport k et, B et C deux points du plan d'image respective M et N par cette homothétie.
Les points A, B, C, M et N forment une configuration de Thalès car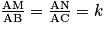 .
.
Les points A, B, C, M et N forment une configuration de Thalès car
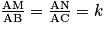 .
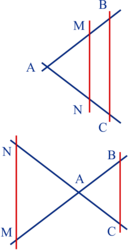
.Si k > 0, c'est la configuration de la figure 1 et, si k < 0, c'est la configuration de la figure 2.
 |
Exercice n°1
Soit h une homothétie de centre O et le point M' l'image d'un point M par h.
Les points O, M et M' sont alignés.
Les points O, M et M' sont alignés.
Cochez la bonne réponse.
| ||
|
Vrai. Par définition, un point et son image par une homothétie sont alignés avec le centre de cette homothétie.
En effet, en notant k le rapport de l'homothétie, si k > 0, M'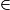 [OM) et si k < 0, M'
[OM) et si k < 0, M'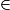 [MO).
[MO).
Dans tous les cas, M'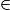 (OM), donc les points O, M et M' sont alignés.
(OM), donc les points O, M et M' sont alignés.
En effet, en notant k le rapport de l'homothétie, si k > 0, M'
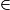 [OM) et si k < 0, M'
[OM) et si k < 0, M'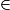 [MO).
[MO).Dans tous les cas, M'
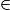 (OM), donc les points O, M et M' sont alignés.
(OM), donc les points O, M et M' sont alignés.Exercice n°2
Quel est le rapport de l'homothétie de centre A qui transforme le point B en le point C ?
 |
Cochez la bonne réponse.
| ||
| ||
|
On a AC = 9 cm = 1,5×6 cm = 1,5AB et C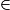 [AB) (B et C sont du même côté par rapport à A) donc :
[AB) (B et C sont du même côté par rapport à A) donc :
Le rapport de l'homothétie de centre A qui transforme le point B en le point C est 1,5.
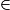 [AB) (B et C sont du même côté par rapport à A) donc :
[AB) (B et C sont du même côté par rapport à A) donc : Le rapport de l'homothétie de centre A qui transforme le point B en le point C est 1,5.
Exercice n°3
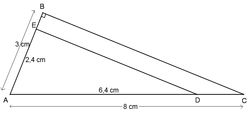
Dans la figure, l'homothétie h1 de centre A transforme le triangle ABC en le triangle AED. Quel est le rapport de cette homothétie ?
 |
Cochez la bonne réponse.
| ||
| ||
|
Dans la figure, on a 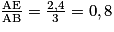 et
et 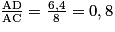 .
.
Il s'agit donc d'une configuration de Thalès et l'homothétie h1 qui transforme le triangle ABC en le triangle AED est une homothétie de centre A qui a pour rapport 0,8.
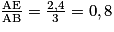 et
et 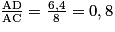 .
.Il s'agit donc d'une configuration de Thalès et l'homothétie h1 qui transforme le triangle ABC en le triangle AED est une homothétie de centre A qui a pour rapport 0,8.
Exercice n°4
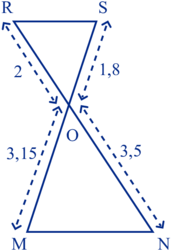
Dans la figure, l'homothétie h2 de centre O transforme le triangle ORS en le triangle ONM. Quel est le rapport de cette homothétie ?
 |
Cochez la bonne réponse.
| ||
| ||
|
Dans la figure, on a 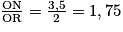 et
et 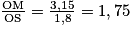 , et R et N ainsi que S et M, sont de part et d'autre de O.
, et R et N ainsi que S et M, sont de part et d'autre de O.
Il s'agit donc d'une configuration de Thalès et l'homothétie h2 qui transforme le triangle ORS en le triangle ONM est une homothétie de centre O qui a pour rapport −1,75.
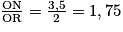 et
et 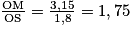 , et R et N ainsi que S et M, sont de part et d'autre de O.
, et R et N ainsi que S et M, sont de part et d'autre de O.Il s'agit donc d'une configuration de Thalès et l'homothétie h2 qui transforme le triangle ORS en le triangle ONM est une homothétie de centre O qui a pour rapport −1,75.