Notion précédente

Effectuer des calculs sur des puissances de 10

Notion suivante
Signaler une erreur
Mathématiques - Réviser une notion
Effectuer des calculs sur des puissances de 10
Vous avez repéré une erreur, une faute d'orthographe, une réponse erronée... Décrivez-nous le problème et nous nous chargerons de le corriger.
Imprimer
Mathématiques - Réviser une notion
Effectuer des calculs sur des puissances de 10
Choisir ce que vous souhaitez imprimer :
Imprimer
Cas d'une multiplication
On additionne les exposants :
102 × 103 = 102 + 3 = 105.
Cas d'une division
On soustrait les exposants :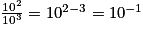
\frac{10^2}{10^3} = 10^{2-3} = 10^{-1}.
Cas d'une puissance de puissance
On multiplie les exposants :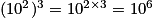
(10^2)^3 = 10^{2\times3} = 10^6.
Exercice n°1
Coche la bonne réponse.
a. 103 × 105 =
Cochez la bonne réponse.
1015
108
b. 103 × 10−5 =
Cochez la bonne réponse.
10−15
10−2
c. 10−3 × 10−5 =
Cochez la bonne réponse.
1015
10−8
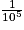
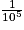
d. \frac{1}{10^5}
Cochez la bonne réponse.
10−5
105
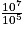
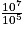
e. \frac{10^7}{10^5}
Cochez la bonne réponse.
1012
102
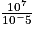
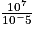
f. \frac{10^7}{10^-5}
Cochez la bonne réponse.
1012
102
Lorsqu'on multiplie des puissances d'un même nombre, on ajoute les exposants.
Lorsqu'on divise des puissances d'un même nombre, on soustrait les exposants.
Exercice n°2
Coche la bonne réponse.
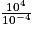\frac{10^4}{10^{-4}} est égal à 1.
Cochez la bonne réponse.
vrai
faux
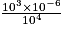\frac{10^3 \times 10^{-6}}{10^4} est égal à 10.
Cochez la bonne réponse.
vrai
faux
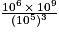\frac{10^6 \, \times \, 10^9}{(10^5)^3}est égal à 1.
Cochez la bonne réponse.
vrai
faux
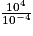• \frac{10^4}{10^{-4}} = 10^{4 - (-4)} = 10^{4 + 4} = 10^8.
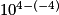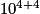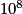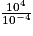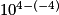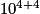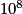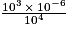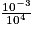• \frac{10^3 \, \times \, 10^{-6}}{10^4} = \frac{10^{-3}}{10^4} = 10^{-3 - 4} = 10^{-7}.
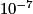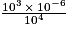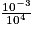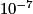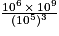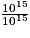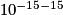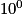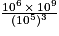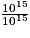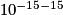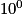• \frac{10^6 \, \times \, 10^9}{(10^5)^3} = \frac{10^{15}}{10^{15}} = 10^{-15 - 15} = 10^0 = 1.
Signaler une erreur
Mathématiques - Réviser une notion
Effectuer des calculs sur des puissances de 10
Vous avez repéré une erreur, une faute d'orthographe, une réponse erronée... Décrivez-nous le problème et nous nous chargerons de le corriger.
Imprimer
Mathématiques - Réviser une notion
Effectuer des calculs sur des puissances de 10
Choisir ce que vous souhaitez imprimer :
Imprimer
un partenariat
Nos sites
Mon espace éducation
Cap Concours
Il était une histoire
Apprendre à porter secours
La quinte juste
Les solutions éducatives MAIF
Le fonds MAIF pour l'éducation
L'espace enseignant MAIF
Informations légales Contact © 2000-2025, rue des écoles