Nouveau message
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Signaler une erreur
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Imprimer
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Méthode pour multiplier un nombre décimal…
• Par 10n, avec n > 0 :
On déplace la virgule de n rangs vers la droite :
3,845 × 102 = 384,5
3,845 × 104 = 38 450
On déplace la virgule de n rangs vers la droite :
3,845 × 102 = 384,5
3,845 × 104 = 38 450
• Par 10−n, avec n > 0 :
On déplace la virgule de n rangs vers la gauche :
384,5 × 10−2 = 3,845
384,5 × 10−4 = 0,038 45
On déplace la virgule de n rangs vers la gauche :
384,5 × 10−2 = 3,845
384,5 × 10−4 = 0,038 45
Application
Un nombre décimal peut s'écrire sous différentes formes qui font intervenir une puissance de 10.
| 415 000 | = 41 500 × 10 |
| = 4 150 × 102 | |
| = 415 × 103 |
| 0,004 15 | = 0,041 5 × 10−1 |
| = 0,415 × 10−2 | |
| = 4,15 × 10−3 |
Exercice n°1
Écris les nombres suivants sous forme décimale.
Écrivez les réponses dans les zones colorées.
a. 3,45 × 105 = 345000|345 000
b. 345 × 10−2 = 3,45|3.45
c. 3,451 × 10−3 = 0,003451|0.003451|0,003 451|0.003 451
d. 3,451 × 102 = 345,1|345.1
a. Multiplier un nombre par 105 revient à déplacer la virgule de 5 rangs vers la droite.
b. Multiplier un nombre par 10−2 revient à déplacer la virgule de 2 rangs vers la gauche. Etc.
Exercice n°2
Coche la bonne réponse.
12 × 107 × 15 × 104 est égal à 27 × 1011.
Cochez la bonne réponse.
| ||
|
12 × 107 + 15 × 104 est égal à 27 × 1011.
Cochez la bonne réponse.
| ||
|
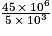est égal à 9 000. Cochez la bonne réponse.
| ||
|
• 12 × 107 × 15 × 104 = (12 × 15) × 107 × 104 = 180 × 107 + 4 = 180 × 1011.
• 12 × 107 + 15 × 104 = 12 × 104 × 103 + 15 × 104 = 104(12 000 + 15) = 12 015 × 104.
• 
= 
× 
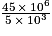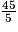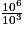= 9 × 103 = 9 000.
= × = 9 × 103 = 9 000.
Nouveau message
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Mathématiques - Réviser une notion
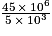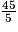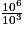Multiplier un nombre décimal par une puissance de 10
Signaler une erreur
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Imprimer
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
Mathématiques - Réviser une notion
Multiplier un nombre décimal par une puissance de 10
