Notion précédente

Faire une division avec des nombres relatifs

Notion suivante
Nouveau message
Mathématiques - Réviser une notion
Faire une division avec des nombres relatifs
Signaler une erreur
Mathématiques - Réviser une notion
Faire une division avec des nombres relatifs
Vous avez repéré une erreur, une faute d'orthographe, une réponse erronée... Signalez-nous la et nous nous chargerons de la corriger.
Imprimer
Mathématiques - Réviser une notion
Faire une division avec des nombres relatifs
Choisir ce que vous souhaitez imprimer :
Imprimer
Cas d'une division en écriture décimale
On applique la règle des signes.
• Le quotient de deux nombres de même signe est positif.
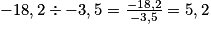
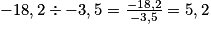
-18,2 \div -3,5 = \frac{-18,2}{-3,5} = 5,2
• Le quotient de deux nombres de signes contraires est négatif.
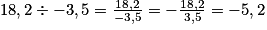
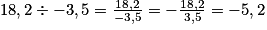
18,2 \div -3,5 = \frac{18,2}{-3,5} = -\frac{18,2}{3,5} = -5,2
Cas d'une division en écriture fractionnaire
On transforme la division en une multiplication par l'inverse et on applique la règle des signes.
• 1er exemple :
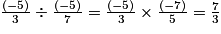
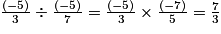
\frac{(-5)}{3} \div \frac{(-5)}{7} = \frac{(-5)}{3} \times \frac{(-7)}{5} = \frac{7}{3}
• 2e exemple :
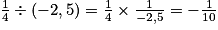
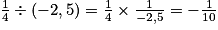
\frac{1}{4} \div (-2,5) = \frac{1}{4} \times \frac{1}{-2,5} = -\frac{1}{10}
Exercice n°1
Coche la bonne réponse.
Le quotient d'un nombre par son opposé est négatif.
Cochez la bonne réponse.
vrai
faux
Le quotient d'un nombre par son inverse est positif.
Cochez la bonne réponse.
vrai
faux
Le quotient et le produit de deux nombres de même signe sont négatifs.
Cochez la bonne réponse.
vrai
faux
Un nombre et son inverse sont de même signe.
• Un nombre et son opposé sont de signe contraire, donc leur quotient est négatif.
• Un nombre et son inverse sont de même signe, donc leur quotient est positif.
• Le quotient et le produit de deux nombres de même signe sont positifs.
Nouveau message
Mathématiques - Réviser une notion
Faire une division avec des nombres relatifs
Signaler une erreur
Mathématiques - Réviser une notion
Faire une division avec des nombres relatifs
Vous avez repéré une erreur, une faute d'orthographe, une réponse erronée... Signalez-nous la et nous nous chargerons de la corriger.
Imprimer
Mathématiques - Réviser une notion
Faire une division avec des nombres relatifs
Choisir ce que vous souhaitez imprimer :
Imprimer
un partenariat
Nos sites
Mon espace éducation
Cap Concours
Il était une histoire
Apprendre à porter secours
La quinte juste
Les solutions éducatives MAIF
Le fonds MAIF pour l'éducation
L'espace enseignant MAIF
Informations légales Contact © 2000-2024, rue des écoles