Signaler une erreur
Mathématiques - Réviser une notion
Multiplier des nombres relatifs
Mathématiques - Réviser une notion
Multiplier des nombres relatifs
Imprimer
Mathématiques - Réviser une notion
Multiplier des nombres relatifs
Mathématiques - Réviser une notion
Multiplier des nombres relatifs
La règle des signes
• Le produit de deux nombres de même signe est positif.
7,2 × 3 = 21,6
− 7,2 × (−3) = 21,6
7,2 × 3 = 21,6
− 7,2 × (−3) = 21,6
• Le produit de deux nombres de signes contraires est négatif.
7,2 × (−3) = −21,6
−7,2 × 3 = −21,6
7,2 × (−3) = −21,6
−7,2 × 3 = −21,6
Application
Quand le produit comprend beaucoup de facteurs, on commence par compter ceux qui sont négatifs. S'il y a un nombre impair de nombres négatifs, le produit est négatif.
Par exemple, le produit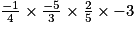 
comprend trois facteurs négatifs.
Son produit est donc négatif :
.
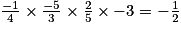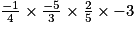comprend trois facteurs négatifs.Son produit est donc négatif :
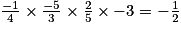.Exercice n°1
Coche la bonne réponse.
Le produit d'un nombre par son opposé est négatif.
Cochez la bonne réponse.
| ||
|
Le produit d'un nombre par son inverse est positif.
Cochez la bonne réponse.
| ||
|
Le produit de 2002 facteurs égaux à − 1 est égal à − 1.
Cochez la bonne réponse.
| ||
|
Un nombre et son inverse sont de même signe.
• Un nombre et son opposé sont de signe contraire, donc leur produit est négatif.
• Un nombre et son inverse sont de même signe, donc leur produit est positif.
• Le nombre de facteurs est pair, donc le produit est positif. Sa valeur est égale à 1.
Signaler une erreur
Mathématiques - Réviser une notion
Multiplier des nombres relatifs
Mathématiques - Réviser une notion
Multiplier des nombres relatifs
Imprimer
Mathématiques - Réviser une notion
Multiplier des nombres relatifs
Mathématiques - Réviser une notion
Multiplier des nombres relatifs
