Énoncé : un camion pesant à vide deux tonnes doit passer sur un pont limité à 6 tonnes.
Combien de caisses de 118 kg peut-il transporter ?
Combien de caisses de 118 kg peut-il transporter ?
Choix de l'inconnue
Soit x le nombre de caisses, on a :
Chargement du camion : 118x.
Poids total du camion : 118x + 2 000
(le camion à vide pèse 2 t).
(le camion à vide pèse 2 t).
Mise en inéquation
On sait que le poids du camion ne doit pas dépasser 6 tonnes.
On peut traduire cette donnée par l'inéquation :
118x + 2 000
6 000.
118x + 2 000
6 000.Résolution de l'inéquation
118 x 4 000
x 4 000 ÷ 118
x 33,89...
4 000x
4 000 ÷ 118x
33,89...Réponse à la question
Le nombre de caisses doit être inférieur ou égal à 33.
Exercice n°1
 |
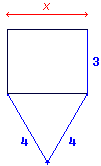Pour quelles valeurs de x le périmètre du rectangle est-il plus grand que celui du triangle isocèle ?
Complète l'inéquation, puis résous-la.
Complète l'inéquation, puis résous-la.
Écrivez les réponses dans les zones colorées.
1. L'inéquation à résoudre est :
2x + > x + .
2x + > x + .
2. Elle équivaut à :
x > .
x > .
• Périmètre du rectangle :
2 (x + 3) = 2x + 6.
2 (x + 3) = 2x + 6.
• Périmètre du triangle :
4 + 4 + x = 8 + x.
4 + 4 + x = 8 + x.
• L'inéquation est donc : 2x + 6 > x + 8.
Soit 2x − x > 8 − 6, d'où x > 2.
Soit 2x − x > 8 − 6, d'où x > 2.
Exercice n°2
Un carré a pour côté 2x − 7. Un triangle équilatéral a pour côté x + 4.
Pour quelles valeurs de x le périmètre du carré est-il strictement supérieur à celui du triangle équilatéral ?
Pour quelles valeurs de x le périmètre du carré est-il strictement supérieur à celui du triangle équilatéral ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Calcule le périmètre du carré en multipliant le côté par 40 et le périmètre du triangle équilatéral en multipliant son côté par 3.
• Le périmètre du carré est 4(2x − 7).
• Le périmètre du triangle équilatéral est 3(x + 4).
• Résous l'inéquation :
4(2x − 7) > 3(x + 4)
8x− 28 > 3x + 12
5x > 40
x > 8.
4(2x − 7) > 3(x + 4)
8x− 28 > 3x + 12
5x > 40
x > 8.
• Les valeurs de x sont toutes celles qui sont strictement supérieures à 8.
Exercice n°3
Quels sont les nombres dont le double est strictement supérieur à leur triple ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
|
Le double du nombre x s'écrit 2x.
• Appelle x les nombres cherchés. Le double du nombre x s'écrit 2x ; le triple du nombre x s'écrit 3x.
• Résous l'inéquation :
2x > 3x
2x − 3x > 0
−x > 0
x < 0.
2x > 3x
2x − 3x > 0
−x > 0
x < 0.
• Les nombres cherchés sont les nombres strictement négatifs.
